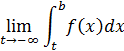Теорема о скачке гладкой функции на ориентированном отрезке:
Скачок гладкой функции  на ориентированном отрезке
на ориентированном отрезке 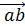 равен интегралу от единицы вдоль
равен интегралу от единицы вдоль  по этому отрезку:
по этому отрезку:

Доказательство:
Это следует из формулы Ньютона-Лейбница, если положить  ′,
′,  .
.
Следствия:
Функция  является гладкой тогда и только тогда, когда она представима в виде интеграла с переменным верхним пределом от некоторой непрерывной функции
является гладкой тогда и только тогда, когда она представима в виде интеграла с переменным верхним пределом от некоторой непрерывной функции 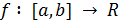 :
:
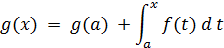
Доказательство.
В качестве  нужно взять производную
нужно взять производную  функции
функции  , доопределенную произ-вольным образом в точках недифференцируемости
, доопределенную произ-вольным образом в точках недифференцируемости  .
.
Докажите теорему об интегрировании по частям для определенного интеграла.
Теорема об интегрировании по частям для определённого интеграла:
Если  и
и  – гладкие функции на ориентированном отрезке
– гладкие функции на ориентированном отрезке 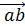 , то
, то

Доказательство:
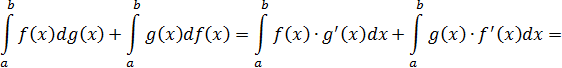

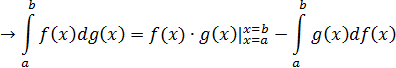
Дайте определение несобственного интеграла по конечному промежутку и по бесконечному промежутку. Докажите теоремы о несобственных интегралах степенной и показательной функций.
Определения:
Локально интегрируемая функция:
Функция  называется локально интегрируемой на множестве
называется локально интегрируемой на множестве  , если она определена на
, если она определена на  и интегрируема на любом отрезке
и интегрируема на любом отрезке  , содержащемся в
, содержащемся в  .
.
Несобственный интеграл по конечному промежутку:
Пусть функция  локально интегрируема на полуинтервале
локально интегрируема на полуинтервале  , где
, где 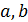 – произвольные числа. Тогда предел
– произвольные числа. Тогда предел
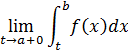
называется несобственным интегралом от f по конечному промежутку (a; b] и обозначается:

Если этот предел существует и конечен, то говорят, что несобственный интеграл сходится, а если не существует или бесконечен, то говорят, что несобственный интеграл расходится.
• Аналогично, если  локально интегрируема на полуинтервале
локально интегрируема на полуинтервале  , то предел
, то предел

называется несобственным интегралом от f по конечному промежутку [a; b) и обозначается

и опять если этот предел существует и конечен, то говорят, что несобственный интеграл сходится, а если не существует или бесконечен, то говорят, что несобственный интеграл расходится.
Несобственный интеграл по бесконечному промежутку:
Пусть функция  локально интегрируема на полуинтервале
локально интегрируема на полуинтервале 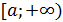 , где
, где  – произвольное число. Тогда предел
– произвольное число. Тогда предел

называется несобственным интегралом от  по бесконечному промежутку
по бесконечному промежутку 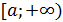 и обозначается
и обозначается

Если этот предел существует и конечен, то говорят, что несобственный интеграл сходится, а если не существует или бесконечен, то говорят, что несобственный интеграл расходится.
• Аналогично, если  локально интегрируема на полуинтервале
локально интегрируема на полуинтервале  , то предел
, то предел
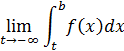
называется несобственным интегралом от  по бесконечному промежутку
по бесконечному промежутку  и обозначается
и обозначается

и опять если этот предел существует и конечен, то говорят, что несобственный интеграл сходится, а если не существует или бесконечен, то говорят, что несобственный интеграл расходится.
Теоремы:
Теорема о несобственном интеграле степенной функции:



Теорема о несобственном интеграле показательной функции:




 на ориентированном отрезке
на ориентированном отрезке 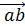 равен интегралу от единицы вдоль
равен интегралу от единицы вдоль 
 ′,
′,  .
. является гладкой тогда и только тогда, когда она представима в виде интеграла с переменным верхним пределом от некоторой непрерывной функции
является гладкой тогда и только тогда, когда она представима в виде интеграла с переменным верхним пределом от некоторой непрерывной функции 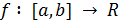 :
: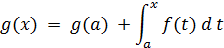
 нужно взять производную
нужно взять производную  функции
функции 
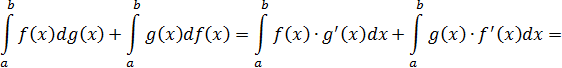

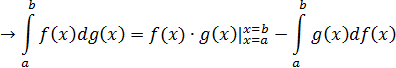
 , если она определена на
, если она определена на  , содержащемся в
, содержащемся в  , где
, где 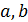 – произвольные числа. Тогда предел
– произвольные числа. Тогда предел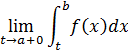

 , то предел
, то предел
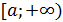 , где
, где  – произвольное число. Тогда предел
– произвольное число. Тогда предел

 , то предел
, то предел