Исследование функции с помощью второй производной
Критическими точками второго рода функции 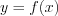 называют те значения аргумента, при которых вторая производная этой функции равна нулю или не существует.
называют те значения аргумента, при которых вторая производная этой функции равна нулю или не существует.
Критические точки второго рода функции 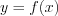 находят, решая уравнение
находят, решая уравнение 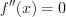 .
.
Если при переходе через критическую точку второго рода вторая производная функции меняет знак, то имеем точку перегиба графика функции.
Если на некотором промежутке выполняется неравенство 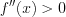 , то функция
, то функция 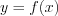 вогнута на этом промежутке, а если
вогнута на этом промежутке, а если 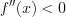 , то функция выпукла на этом промежутке.
, то функция выпукла на этом промежутке.
Билет №40. Наибольшее и наименьшее значение ф-и на промежутке.
Если функция 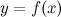 определена и непрерывна на отрезке
определена и непрерывна на отрезке 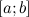 , то она на этом отрезке достигает своих наибольшего и наименьшего значений. Если свое наибольшее значение
, то она на этом отрезке достигает своих наибольшего и наименьшего значений. Если свое наибольшее значение 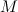 функция
функция  принимает в точке
принимает в точке 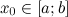 , то
, то 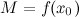 будет локальным максимумом функции
будет локальным максимумом функции  , так как в этом случае существует окрестность точки
, так как в этом случае существует окрестность точки 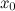 , такая, что
, такая, что 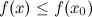 .
.
Однако свое наибольшее значение 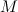 функция
функция  может принимать и на концах отрезка
может принимать и на концах отрезка 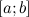 . Поэтому, чтобы найти наибольшее значение
. Поэтому, чтобы найти наибольшее значение 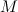 непрерывной на отрезке
непрерывной на отрезке 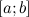 функции
функции  , надо найти все максимумы функции на интервале
, надо найти все максимумы функции на интервале 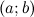 и значения
и значения  на концах отрезка
на концах отрезка 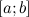 , то есть
, то есть 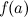 и
и 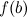 , и выбрать среди них наибольшее. Вместо исследования на максимум можно ограничиться нахождением значений функции в критических точках.
, и выбрать среди них наибольшее. Вместо исследования на максимум можно ограничиться нахождением значений функции в критических точках.
Наименьшим значением 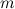 непрерывной на отрезке
непрерывной на отрезке 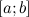 функции
функции  будет наименьший минимум среди всех минимумов функции
будет наименьший минимум среди всех минимумов функции  на интервале
на интервале 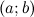 и значений
и значений 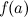 и
и 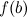 .
.
Билет №41. Направление выпуклости и точки перегиба гр-ка ф-и.
рафик функции 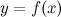 , дифференцируемой на интервале
, дифференцируемой на интервале 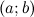 , является на этом интервале выпуклым, если график этой функции в пределах интервала
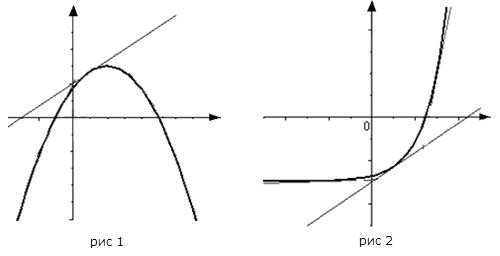
, является на этом интервале выпуклым, если график этой функции в пределах интервала 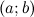 лежит не выше любой своей касательной (рис. 1).
лежит не выше любой своей касательной (рис. 1).
График функции 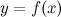 , дифференцируемой на интервале
, дифференцируемой на интервале 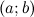 , является на этом интервале вогнутым, если график этой функции в пределах интервала
, является на этом интервале вогнутым, если график этой функции в пределах интервала 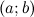 лежит не ниже любой своей касательной (рис. 2).
лежит не ниже любой своей касательной (рис. 2).
Теоремы о выпуклости функции и точках перегиба
Теорема
(Об условиях выпуклости или вогнутости графика функции)
Пусть функция 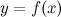 определена на интервале
определена на интервале 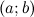 и имеет непрерывную, не равную нулю в точке
и имеет непрерывную, не равную нулю в точке 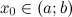 вторую производную. Тогда, если
вторую производную. Тогда, если 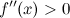 всюду на интервале
всюду на интервале 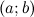 , то функция имеет вогнутость на этом интервале, если
, то функция имеет вогнутость на этом интервале, если 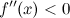 , то функция имеет выпуклость.
, то функция имеет выпуклость.
Определение
Точкой перегиба графика функции 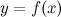 называется точка
называется точка 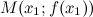 , разделяющая промежутки выпуклости и вогнутости.
, разделяющая промежутки выпуклости и вогнутости.
(О необходимом условии существования точки перегиба)
Если функция 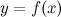 имеет перегиб в точке
имеет перегиб в точке 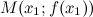 , то
, то 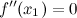 или не существует.
или не существует.
Теорема
(О достаточном условии существования точки перегиба)
Если:
1. первая производная 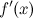 непрерывна в окрестности точки
непрерывна в окрестности точки 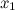 ;
;
2. вторая производная 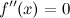 или не существует в точке
или не существует в точке 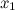 ;
;
3. 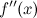 при переходе через точку
при переходе через точку 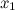 меняет свой знак,
меняет свой знак,
тогда в точке 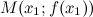 функция
функция 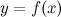 имеет перегиб.
имеет перегиб.



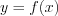 называют те значения аргумента, при которых вторая производная этой функции равна нулю или не существует.
называют те значения аргумента, при которых вторая производная этой функции равна нулю или не существует.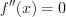 .
.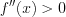 , то функция
, то функция 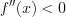 , то функция выпукла на этом промежутке.
, то функция выпукла на этом промежутке.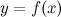 определена и непрерывна на отрезке
определена и непрерывна на отрезке 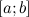 , то она на этом отрезке достигает своих наибольшего и наименьшего значений. Если свое наибольшее значение
, то она на этом отрезке достигает своих наибольшего и наименьшего значений. Если свое наибольшее значение 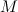 функция
функция  принимает в точке
принимает в точке 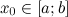 , то
, то 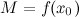 будет локальным максимумом функции
будет локальным максимумом функции 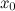 , такая, что
, такая, что 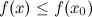 .
.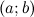 и значения
и значения 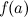 и
и 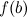 , и выбрать среди них наибольшее. Вместо исследования на максимум можно ограничиться нахождением значений функции в критических точках.
, и выбрать среди них наибольшее. Вместо исследования на максимум можно ограничиться нахождением значений функции в критических точках.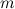 непрерывной на отрезке
непрерывной на отрезке 
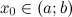 вторую производную. Тогда, если
вторую производную. Тогда, если 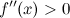 всюду на интервале
всюду на интервале 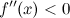 , то функция имеет выпуклость.
, то функция имеет выпуклость.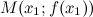 , разделяющая промежутки выпуклости и вогнутости.
, разделяющая промежутки выпуклости и вогнутости.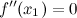 или не существует.
или не существует.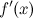 непрерывна в окрестности точки
непрерывна в окрестности точки 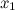 ;
;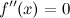 или не существует в точке
или не существует в точке 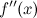 при переходе через точку
при переходе через точку 


