Действия над комплексными числами

 В ПОКАЗАТЕЛЬНОЙ ФОРМЕ

 

Цель:

- сформировать умения выполнения действий над комплексными числами в показательной форме;

- развить навыки преобразований комплексных чисел из алгебраической формы в показательную и наоборот;

- закрепить знания о свойствах тригонометрических функций;

Материально – техническое обеспечение: методические указания по выполнению работы, таблица значений тригонометрических функций;

Время выполнения: 2 академических часа;

Ход занятия:

1. Изучить краткие теоретические сведения;

2. Выполнить задания;

3. Сделать вывод по работе;

4. Подготовить защиту работы по контрольным вопросам.

 Краткие теоретические сведения:

Для представления комплексного числа 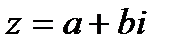 в показательной форме необходимо найти его модуль и главное значение аргумента.

Пример 1. Представить в показательной форме число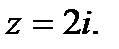

Решение:

Здесь  а = 0, b = 2. Находим модуль по формуле .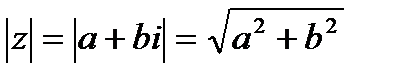

| z| = |2 i| =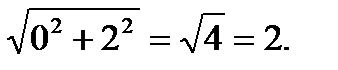

Точка, изображающая число z, лежит в I четверти, тогда 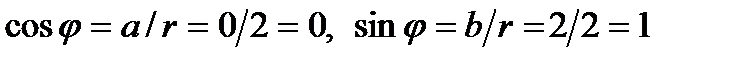. Определим по таблице значений тригонометрических функций главное значение аргумента: 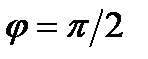. Поэтому, показательная форма числа  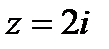согласно формуле 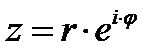примет вид:

.

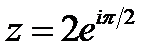Пример 2. Возвести в степень 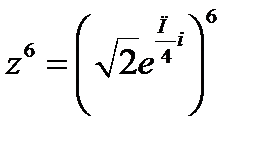 в показательной форме.

Решение:

Для возведения в степень числа 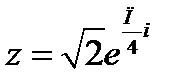 используем формулу  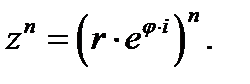Получим: .

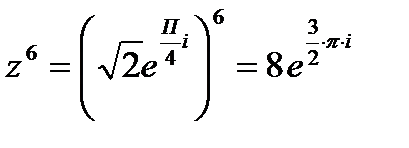Пример 3. Извлечь корень из числа: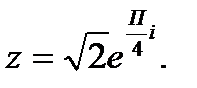

Решение:

   По формуле получим:

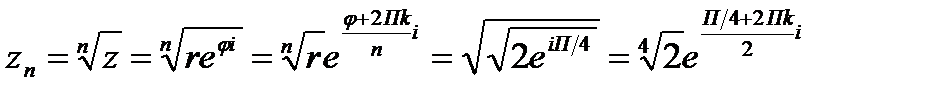
если 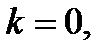 то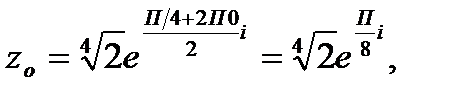

если 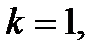 то .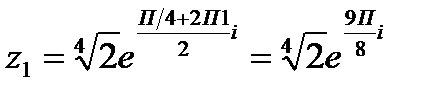

Задания для самостоятельного выполнения:

  I. Представьте комплексное число в  показательной форме.

  II. Переведите комплексное число из тригонометрической формы в показательную и возведите  в степень.               

III. Найдите значение корня в показательной форме.

 

Вариант 1.

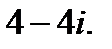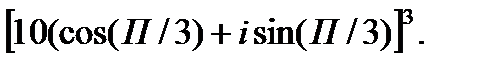1.                       2.                        3.                  

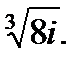
Вариант 2.

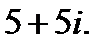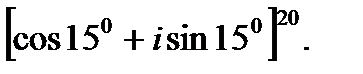1.                       2.                                   3.         

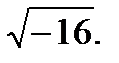
Вариант 3.

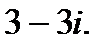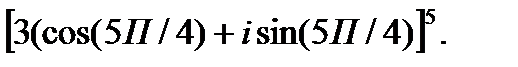1.                       2.                       3.                 

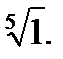
Вариант 4.

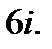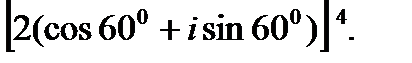1.                           2.                                3.            

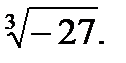
Вариант 5.

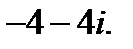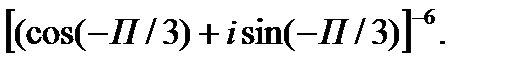1.                    2.                        3.   

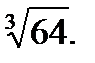
Вариант 6.

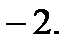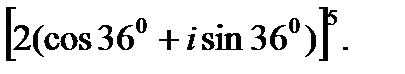1.                         2.                                 3.              

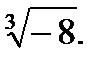
Вариант 7.

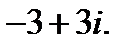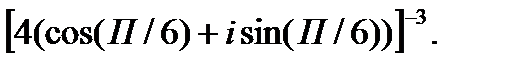1.                    2.                         3.                  

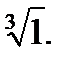
Вариант 8.

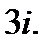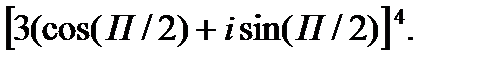1.                           2.                           3.       

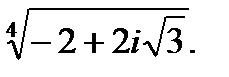
Вариант 9.

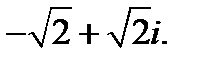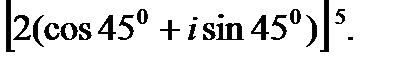1.               2.                                 3.                    

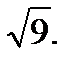
Вариант 10.

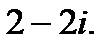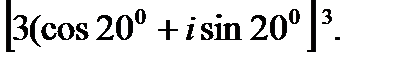1.                      2.                                  3.                  

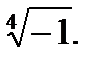
Вариант 11.

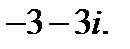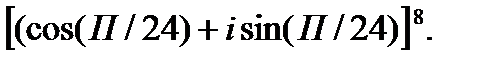1.                    2.                          3.                    

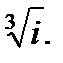
Вариант 12.

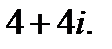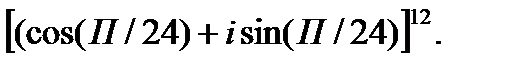1.                      2.                         3.              

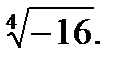
Вариант 13.

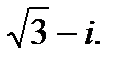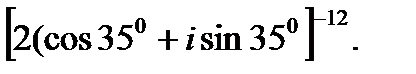1.                     2.                                 3.                

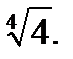
Вариант 14.

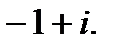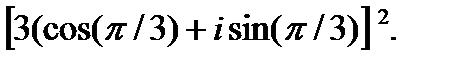1.                     2.                              3.                

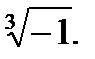
Вариант 15.

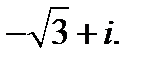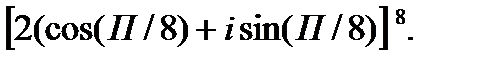1.                   2.                            3.   

 

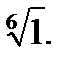
Вопросы для самоконтроля:

1. Какую функцию называют функцией Эйлера?

2. Запишите показательную форму комплексного числа.

3. Как выполняются действия над комплексными числами в показательной форме?

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 4