Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...
Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...
Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Интересное:
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Дисциплины:
 2017-09-10 |
 1816 |
из
5.00
|
Заказать работу |
|
|
|
|
Функция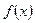 
называется непрерывной в точке 
, если предел функции при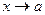 
равен значению функции при :
.
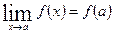А также говорят, функция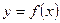 
называется непрерывной в точке , если она в этой точке определена, и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т. е.
.
Существует теорема о непрерывности функции в точке. Функция y= f(x) непрерывна в точке x0, тогда и только тогда, когда функция имеет конечные пределы в точке x0 и предел функции в точке x0 равен значению функции в этой точке.
Все элементарные функции непрерывны в области своего определения.
Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции.
Для элементарных функций справедливы следующие положения:
1. область непрерывности элементарной функции совпадает с её областью определения, т.е. элементарная функция непрерывна во всей области определения
2. элементарная функция может иметь разрыв только в отдельных точках какого-либо промежутка, но не во всех его точках
3. элементарная функция может иметь разрыв только в той точке, в которой она не определена.
Функция называется непрерывной в промежутке (замкнутом или открытом), если она непрерывна во всех точках этого промежутка.
Все точки разрыва функции разделяются на точки разрыва первого и второго рода.
Точка разрыва х0 называется точкой разрыва первого рода функции 
, если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т.е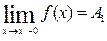 
и 
.
При этом:
если А1=А2, то точка х0 называется точкой устранимого разрыва
если 
, то точка х0 называется точкой конечного разрыва
Величину 
называют скачком функции
Прямая называется асимптотой кривой y=f(x), если расстояние от точки М(x;y) до этой прямой стремится к 0 при стремлении, хотя бы одной из координат к ∞
|
|
Вертикальные асимптоты.
График функци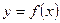и при 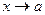имеет вертикальную асимптоту, ес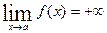ли 
или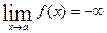 
; при этом точка есть точка разрыва II-го рода. Уравнение вертикальной асимптоты имеет вид .
Горизонтальные асимптоты.
График функци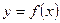и при 
или при 
имеет горизонтальную асимптоту, если 
или 
. Может оказаться, что либо только один из этих пределов конечный, либо ни одного. Тогда график имеет или одну горизонтальную асимптоту, или ни одной. Уравнение горизонтальной асимптоты имеет вид 
(рис. 9).
Рис. 9. Графики функций, имеющие горизонтальные асимптоты
Наклонные асимптоты.
Если существуют пределы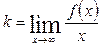 
и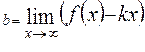 
, то прямая y=kx+b является наклонной асимптотой кривой при указанном стремлении x. При x → 
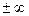асимптоты могут быть различны.
Методы раскрытия неопределенности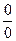 
:
1. Разложение числителя и знаменателя функции на множители с последующим сокращением дроби.
2. Устранение иррациональных разностей. Домножение на сопряженное.
3. Первый замечательный предел 
Задача. Найти 
Решение:
Дробь при 
не вычисляется, причем 
и 
, т.е. дробь представляет собой отношение двух бесконечно малых функций (неопределенность вида 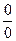). Для вычисления предела дроби (раскрытия неопределенности) следует разложить и числитель, и знаменатель на множители и при наличии одинакового множителя, стремящегося к 0 при 
, дробь на этот множитель сократить: 
.
Для разложения на множители числителя необходимо вспомнить формулу 
, где 
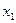и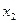 
- действительные корни квадратного трехчлена, 
.
Для трехчлена 
, 
, 
, 
.
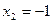Поэтому 
.
Для 
преобразования будут такими:
;
.
Задача. Найти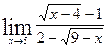 
.
Решение: При х=5 дробь не вычисляется, пределы числителя и знаменателя равны 0, т.е. имеем неопределенность вида 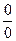. Для раскрытия неопределенности следует избавиться от конкретных иррациональностей в числителе и знаменателе, а при наличии общего множителя дробь на него сократить. Достигается это с помощью следующих тождественных преобразований для 
:
|
|
= 
.
Теперь 
.
Задача. Найти 
.
Решение: Дробь при х=0 не вычисляется 
, 
, имеем неопределенность вида 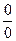. Преобразуем дробь следующим образом: 
.
.
Следует отметить, что если функция 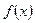есть дробь, числитель который при 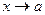имеет предел, отличный от 0, а знаменатель, напротив, имеет пределом 0, то 
.
Задача. Найти 
.
Решение: 
, 
.
Следовательно, 
.
Неопределенность вида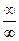 
Используют метод деления на наибольшую степень.
Полезно использовать следующую теорему:
При 
предел отношения двух многочленов равен отношению коэффициентов при высших степенях x этих многочленов, если степень n многочлена числителя равна степени m многочлена знаменателя. Если 
, то предел равен нулю. Если 
, то предел равен бесконечности.
Задача. Найти 
.
Решение: При 
и числитель, и знаменатель – бесконечно большие функции (неопределенность вида 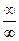). Для раскрытия неопределенности преобразуем дробь, разделив числитель на знаменатель на старшую степень 
, т.е. на 
:
.
Теперь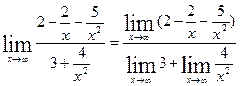 
= 
Задача. Найти 
.
Решение: Имеем неопределенность вида 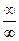. Разделим числитель и знаменатель на 
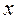. Тогда:
.
Здесь была использована формула: 
.
Задача. Найти предел 
.
Преобразуем это выражение. В каждом из многочленов вынесем множитель х в старшей степени за скобки. Получим:
= 
=
= 
= 
= 
= 
.
Ответ: .
В процессе вычисления предела мы воспользовались теоремами о пределе суммы, произведения, частного, а так же теоремой о делении ограниченной функции на бесконечно большую.
Задача. Найти предел 
.
Данный предел является пределом вида ¥-¥. Умножим и разделим выражение под знаком предела на выражение сопряженное этой сумме 
. Получим
= 
=
= 
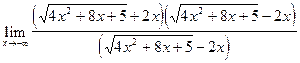=(далее ход решения аналогичен тому, который был использован в предыдущей задаче)= = 
=(заметим, что при х<0 имеем 
)= = 
= 
. Ответ:-2.
Задача. Найти предел
Решение
Здесь неопределенность вида 
. Под знаком предела стоит разность корней второй степени. Для нахождения этого предела умножим и разделим эту разность на выражение, сопряженное этой разности. В результате получим:
Вопросы для самопроверки:
1. Какая функция называется бесконечно малой?
2. Какова связь между бесконечно малой и бесконечно большой функциями?
3. Сформулируйте основные теоремы о пределах.
4. Дайте определение непрерывной функции в точке и на промежутке (а;b).
|
|
|
|
|
Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...
Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...
Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...
Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!