n = Application.Count(xe)
Dim D() As Variant
ReDim D(n, n) As Variant
'конечные разности 1-ого порядка в 1-0м столбце массива d
For i = 1 To n - 1
D(i, 1) = ye(i + 1) - ye(i)
Next i
For j = 2 To n - 1
For i = 1 To j
D(i, j) = D(i + 1, j - 1) - D(i, j - 1)
Next i
h = xe(2) - xe(1)
Next j
ne = ye(1)
For i = 1 To n - 1
p = 1
For j = 1 To i
p = p * (x - xe(j)) / (j * h)
Next j
ne = ne + p * D(1, i)
Next i
Newtonn = ne
End Function
Function Kanon(x As Double, xe As Variant, ye As Variant)
Dim xx() As Double
Dim yye() As Double
n = Application.Count(xe)
ReDim xx(1 To n, 1 To n) As Double
ReDim yye(1 To n, 1 To 1) As Double
For i = 1 To n
For j = 1 To 1
yye(i, j) = ye(i)
Next j
Next i
For i = 1 To n
For j = 1 To n
If j = 1 Then xx(i, j) = xe(i) ^ 0
If j = 2 Then xx(i, j) = xe(i) ^ 1
If j = 3 Then xx(i, j) = xe(i) ^ 2
If j = 4 Then xx(i, j) = xe(i) ^ 3
If j = 5 Then xx(i, j) = xe(i) ^ 4
If j = 6 Then xx(i, j) = xe(i) ^ 5
Next j
Next i
Kanon = 0
For i = 1 To n
Kanon = Kanon + Application.Product(Application.Index(Application.MMult(Application.MInverse(xx), yye), i), x ^ (i - 1))
Next i
End Function
Некоторые комментарии к программам:
модули
– Function lagr(x As Double, xe As Variant, ye As Variant)
– Function Newtonn(x As Double, xe As Variant, ye As Variant)
– Function Kanon(x As Double, xe As Variant, ye As Variant)
обеспечивают вычисления значений интерполяционных полиномов Лагранжа, Ньютона и канонического интерполяционного полинома.
Подпрограмма Private Sub CommandButton1_Click() обеспечивает ввод исходных данных и вызов модулей lagr, Newtonn и Kanon.
Калькулятор поддерживает вычисление значений интерполяционных полиномов степенью не выше пятой, хотя изменения программы для увеличения степени вычисляемых интерполяционных полиномов достаточно просты.
Недостатком рассмотренного калькулятора является то, что при любом изменения данных необходимо снова вводить всю интерполяционную таблицу.
Для вызова второго калькулятора необходимо нажать кнопку Второй калькулятор, рис. 3.4.5.
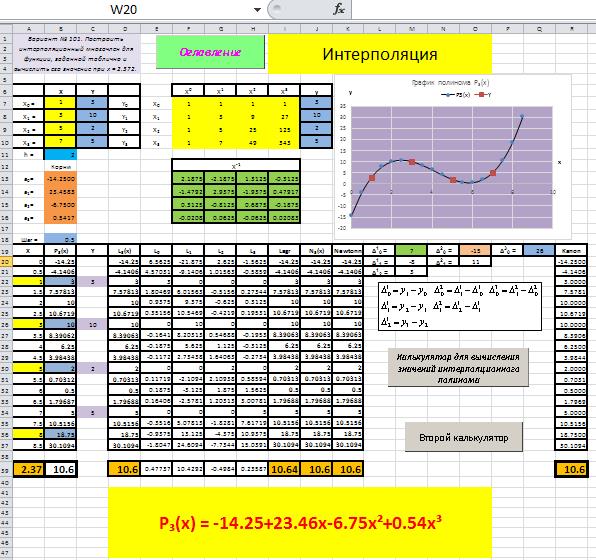
Рис. 3.4.5
На появившейся панели калькулятора Интерполяция нажать кнопку Ввод таблицы, рис. 3.4.6.
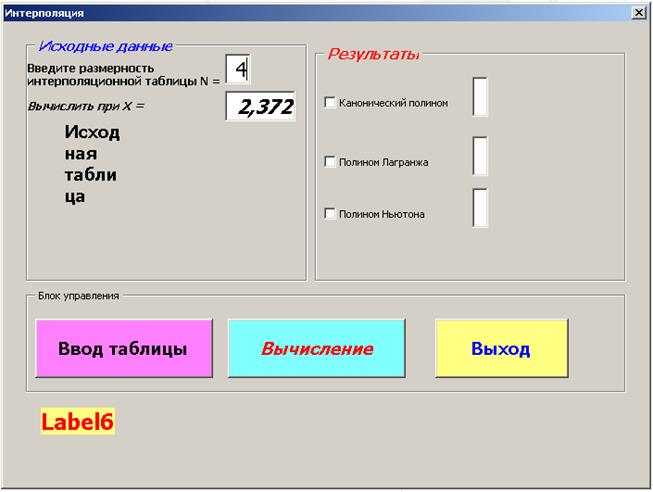
Рис. 3.4.6
В появившемся окне Ввод значений интерполяционной таблицы последовательно вводя значения исходной таблицы варианта задания (а потом и любые другие данные), и нажимая кнопку ОК, сформировать исходную интерполяционную таблицу, рис. 3.4.7.
В окне Ввод значений интерполяционной таблицы для удобства указываются данные соответствующие выполняемому варианту задания.
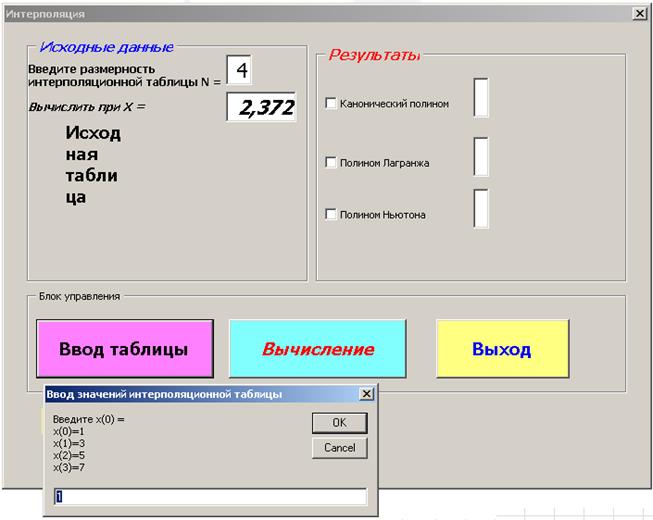
Рис. 3.4.7
После последнего нажатия кнопки ОК появится панель калькулятора Интерполяция, рис. 3.4.8.
На появившейся панели калькулятора Интерполяция включить “флажки” у полиномов, значения которых необходимо вычислить, и нажать кнопку Вычисление, рис. 3.4.8.
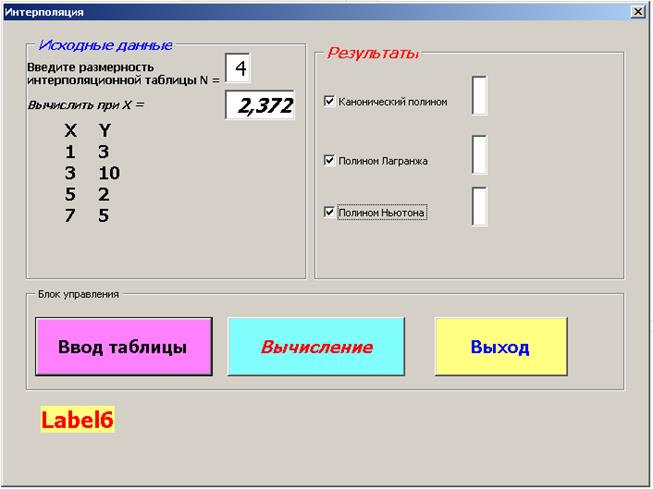
Рис. 3.4.8
Появится панель калькулятора Интерполяция с результатами вычислений, рис. 3.4.9.
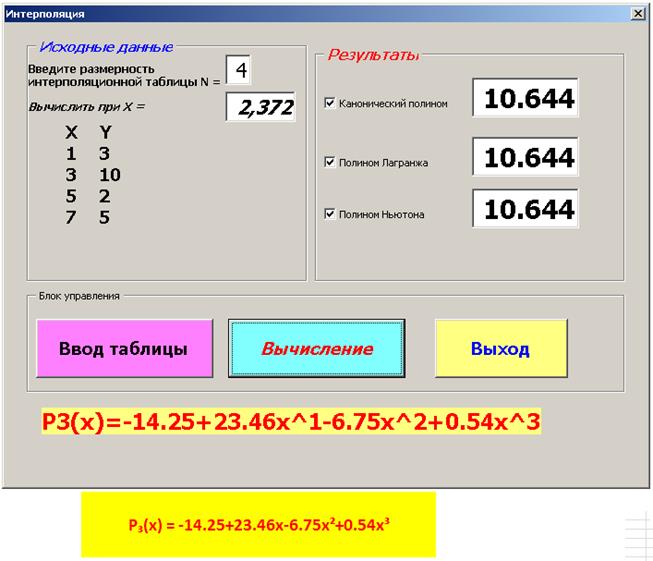
Рис. 3.4.9
Таким образом, для выполняемого варианта задания, при значении Х = 2.372 вычисленное значение канонического интерполяционного полинома, полинома Лагранжа и полинома Ньютона совпадают и равны величине 10.644.
Эти результаты совпадают и с результатами, полученными при вычислениях в среде Excel.
Кроме того, в объекте Label 6 появится аналитическое выражение полинома P 3 (x) = -14.25 + 23.46 x – 6.75 x 2 + 0.54 x 3, записанное в виде P 3(x) = -14.25 + 23.45 x ^1 – 6.75 x ^2 + 0.54 x ^3, также совпадающее с аналитическим выражением интерполяционного полинома, полученного в среде Excel.
Не закрывая панель калькулятора Интерполяция, можно поверить совпадение значений построенного интерполяционного полинома и данных исходной интерполяционной таблицы в узлах интерполяции. При этом достаточно изменять только значение величины X, не перезагружая исходную интерполяционную таблицу.
Работа калькулятора Интерполяция для вычисления значений интерполяционных полиномов поддерживается следующими программными модулями:
Dim xe() As Double
Dim ye() As Double
Dim Aa() As Variant
Dim t As Variant
Private Sub CommandButton2_Click()
Unload Me
End Sub
Private Sub CommandButton3_Click()
Dim x As Double
n = CDbl(TextBox7)
ReDim Preserve xe(1 To n)
ReDim Preserve ye(1 To n)
For i = 1 To n
xe(i) = InputBox("Введите x(" & CStr(i - 1) & ") =" & vbCr & "x(0)=1" & vbCr & "x(1)=3" & vbCr & "x(2)=5" & vbCr & "x(3)=7", " Ввод значений интерполяционной таблицы", 1, 5000, 8000)
Next i
For i = 1 To n
ye(i) = InputBox("Введите y(" & CStr(i - 1) & ") =" & vbCr & "y(0)=3" & vbCr & "y(1)=10" & vbCr & "y(2)=2" & vbCr & "y(3)=5", " Ввод значений интерполяционной таблицы", 1, 8000, 5000)
Next i
Label5 = "X" & " Y" & vbCr & CStr(xe(1)) & " " & CStr(ye(1)) & vbCr & CStr(xe(2)) & " " & CStr(ye(2)) & vbCr & CStr(xe(3)) & " " & CStr(ye(3)) & vbCr & CStr(xe(4)) & " " & CStr(ye(4))
End Sub
Private Sub CommandButton4_Click()
Dim x As Double
Dim nad As String
Dim ziclo As Double
n = CDbl(TextBox7)













