Тема. Вычисление производных. Задачи на исследование функций. Повторение
ЗАДАНИЕ. Изучить материал теоретической части, законспектировать
Вычисление производных проводится по формулам и правилам. Повторяем формулы и правила
Основные правила дифференцирования
Непосредственное вычисление производной функции с помощью предела в большинстве случаев представляет собой громоздкие вычисления. Значительно проще вычислять производные, применяя правила дифференцирования.
Обозначения: С−постоянная; х−аргумент; u, v, w−функции от х, имеющие производные.
Правило 1. Производная постоянной
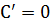
Правило 2. Производная произведения постоянной на функцию
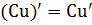
Правило 3. Производная алгебраической суммы
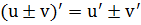
Правило 4. Производная произведения
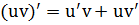
Правило 5. Производная частного (дроби)
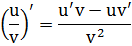
Частные случаи
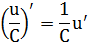
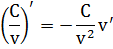
Таблица основных формул дифференцирования
Формулы
Элементарные:
1. С΄ = 0, где С-любое число
2. х΄ = 1
3. (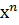 )΄ = n
)΄ = n 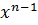
4. (аx+ b)΄ = а
5. ( )΄ =
)΄ = 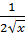
Сложные:
6. ( )΄ = n·(ах+b)ʹ
)΄ = n·(ах+b)ʹ 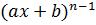
7. (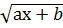 )΄ =
)΄ = 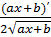
Тригонометрические
8. (sin x)΄ = cos x
9. (cos x)΄ = - sin x
10. (tg x)΄ = 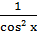
11. (ctg x)΄ = - 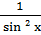
Сложные тригонометрические
12. (sin (kx+b))΄ = k cos (kx+b)
13. (cos (kx+b))΄ = - k sin (kx+b)
14. (tg (kx+b))΄ = 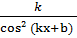
15. (ctg (kx+b))΄ = - 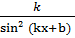
Обратные тригонометрические
16. (arcsin x)΄ = 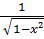
17. (arccos x)΄ = - 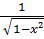
18. (arctg x)΄ = 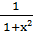
19. (arcctg x)΄ = - 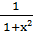
Дополнительные тригонометрические
20. (sin² x)΄ = sin 2x
21. (cos² x)΄ = - sin 2x
Показательные
22. 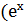 )΄ =
)΄ = 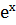
23.  )΄ =
)΄ = 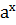
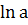
24. (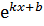 )ʹ = (kx+b)ʹ
)ʹ = (kx+b)ʹ 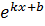
25. (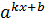 )ʹ = (kx+b)ʹ
)ʹ = (kx+b)ʹ 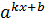 ln a
ln a
Логарифмические
26. ln΄x = 
27. 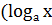 )΄ =
)΄ = 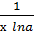
28. (ln(kx+b))ʹ = 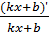 29. (
29. (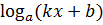 )ʹ =
)ʹ = 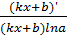
Пример 1. Найти производную функции 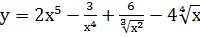 .
.
Решение. Запишем формулу в виде
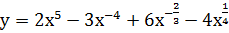
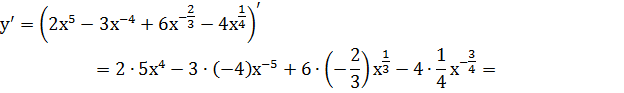
= 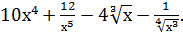
Пример 2. Найти производную функции 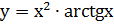 .
.
Решение. Применяя правило производная произведения и формулы (2) и (15) получим
 .
.
Пример 3. Найти производную функции 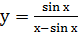 .
.
Решение. Применяя правило производная частного и формулы (1) и (5) получим
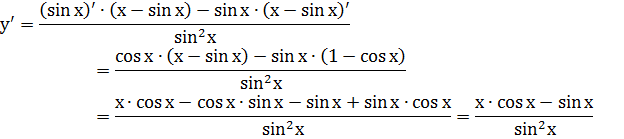
Пример 4. Найти производную 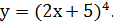
Решение.
y’= 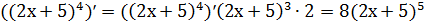 .
.
Пример 5. Найти производную функции y=sin(3x-5).
Решение. 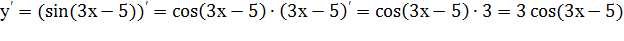 .
.
Пример 6. Найти производную функции у= 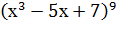 .
.
Решение. 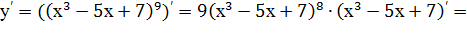
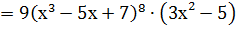 .
.
Пример 7. Найти производную функции у= 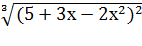 .
.
Решение. Эта функция также является сложной степенной функцией, а именно у= 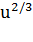 , где u=
, где u=  . Поэтому
. Поэтому
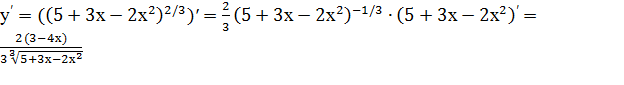 .
.
Пример 8. Найти производную функции у= 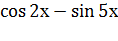 .
.
Решение.
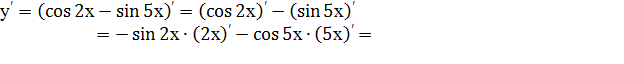
= 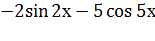 .
.
Пример 9. Дана функция f(x)= 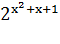 . Найти
. Найти 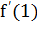 .
.
Решение.
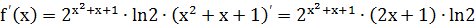 .
.
Вычислим значение производной при х=1
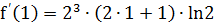 ,
,
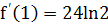 . [1]
. [1]
Применение производной
Применение производной при исследовании функции
На монотонность
Схема исследования ф-и на монотонность:
1) Найти область определения ф-и
2) Найти производную ф-и
3) Решить уравнение f ′(x) = 0
4) Нанести найденные точки (если таковые имеются) на числовой луч (точки
закрашены)
5) Просчитать знаки промежутков (подставляя числа из промежутков в
производную)
6) если «+» - ф-я возрастает
«-» - убывает
7) Если переход знака с «+» на «-» - точка максимума
с «-» на «+» - минимума
Примеры. Исследовать функцию на монотонность:
а) f (x) = 3 – x
x
D (f) = (- ∞; 0) U (0; + ∞)
f ′(x) = (3-x)′ x – (3-x) x′ = - x – 3 + x = - 3
x² x² x²
f ′ (x) = 0 => - 3 ≠ 0
x²
- - x
- ∞ 0 + ∞
Ответ: ф-я убывает (- ∞; 0) и (0; + ∞)
б) f (x) = x - x³
D (f) = R
f ′(x) = 1 – 3 x²
f ′(x) = 0 => 1 – 3x² = 0
- 3x² = - 1
x² = ⅓
x = ± 1/√3
- + - x
- ∞ - 1/√3 1/√3 + ∞
Ответ: ф-я возрастает [- 1/√3; 1/√3], убывает (- ∞; - 1/√3] и [1/√3; + ∞)
На экстремумы.
Схема исследования ф-и на экстремумы:
1) Найти область определения ф-и
2) Найти производную ф-и
3) Решить уравнение f ′(x) = 0
4) Нанести найденные точки (если таковые имеются) на числовой луч (точки закрашены)
5) Просчитать знаки промежутков (подставляя числа из промежутков в производную)
6) Если переход знака с «+» на «-» - точка максимума
с «-» на «+» - минимума
Пример. 1. Найти точки экстремума функции f (x) = 3x - x³
D (f) = R
f ′(x) = 3 – 3 x²
f ′(x) = 0 => 3 – 3x² = 0
- 3x² = - 3
x² = 1
x = ± 1
- + - x
- ∞ - 1 1 + ∞
Ответ: хmax = 1; xmin = - 1.
2.Исследовать функцию на экстремумы f (x) = х² - 6х + 9
х - 1
D (f) = (- ∞; 1) U (1; + ∞)
f ′(x) = (x ² - 6 x + 9)′ (x – 1) - (x ² - 6 x + 9) (x – 1)′ =
(x – 1)²
= (2 x - 6) (x - 1) – (x ² - 6 x + 9) = 2 x ² - 2 x – 6 x + 6 - x ² + 6 x – 9 =
(x - 1)² (x - 1)²
= x² - 2x – 3
(x - 1)²
f ′ (x) = 0 => x² - 2x - 3 = 0
(x – 1)²
x² - 2x – 3 = 0 (x - 1)² ≠ 0
D = 16, X1 = - 1, X2 = 3 x ≠ 1
+ - - + x
- ∞ - 1 1 3 + ∞
xmax = - 1, уmax = (1+6+9)/ (-2) = - 8;
xmin = 3, уmin = (9-18+9)/2 = 0
Ответ: хmax = - 1, уmax = - 8; хmin = 3, уmin = 0
Тема. Вычисление производных. Задачи на исследование функций. Повторение
ЗАДАНИЕ. Изучить материал теоретической части, законспектировать
Вычисление производных проводится по формулам и правилам. Повторяем формулы и правила



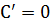
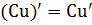
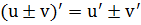
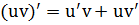
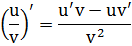
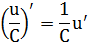
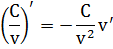
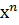 )΄ = n
)΄ = n 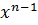
 )΄ =
)΄ = 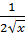
 )΄ = n·(ах+b)ʹ
)΄ = n·(ах+b)ʹ 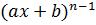
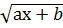 )΄ =
)΄ = 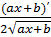
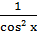
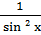
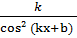
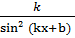
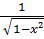
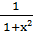
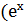 )΄ =
)΄ = 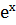
 )΄ =
)΄ = 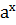
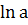
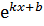 )ʹ = (kx+b)ʹ
)ʹ = (kx+b)ʹ 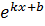
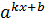 )ʹ = (kx+b)ʹ
)ʹ = (kx+b)ʹ 
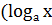 )΄ =
)΄ = 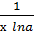
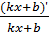 29. (
29. (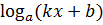 )ʹ =
)ʹ = 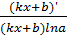
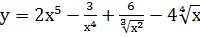 .
.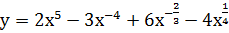
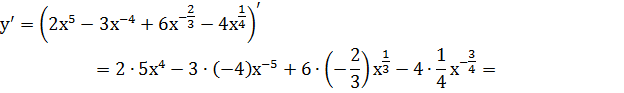
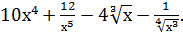
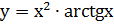 .
. .
.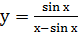 .
.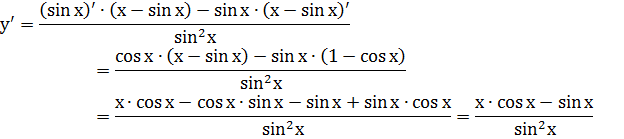
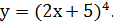
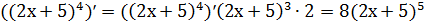 .
.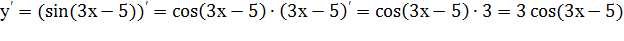 .
.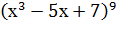 .
.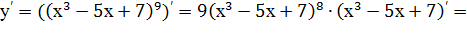
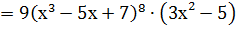 .
.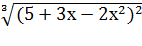 .
.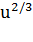 , где u=
, где u=  . Поэтому
. Поэтому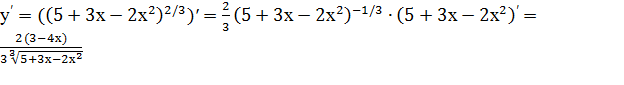 .
.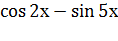 .
.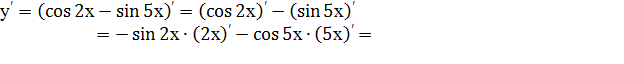
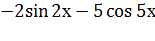 .
.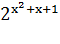 . Найти
. Найти 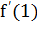 .
.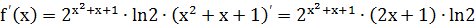 .
.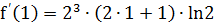 ,
,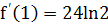 . [1]
. [1]


