Максимальные ЛРП.
Определение 1. Последовательность d = {d x } Î s называется периодической, если существует такое неотрицательное число k, и такое натуральное числоt, что для всех x Î N 0, x ³ k выполняется равенство d x + t = d x.
Наименьшие натуральные числа k и t, удовлетворяющие условиям определения 1 называются соответственно, периодом и длиной предпериода последовательности d.
Периодическую последовательность можно изобразить графически следующим образом:
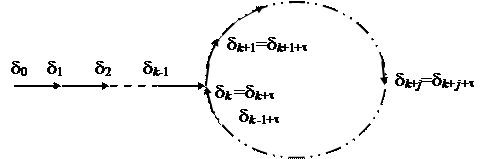
Условие периодичности последовательности эквивалентно условию
Tk + t·d = Tk ·d, Tk + t·d - Tk ·d = 0,
или
l k (l t -1)·d = 0. (1)
Обозначим через k (d) и t(d) соответственно длину предпериода и периода последовательности d.
Теорема 1. Пусть d - периодическая последовательность элементов поля F и k Î N 0, t Î N. Тогда условие
для всех x Î N 0, x ³ k равенство d x + t = d x (2)
равносильно условию
k ³ k (d), t(d)| t. (3)
Доказательство. Пусть k 0= k (d), t 0= t(d).Тогда в силу сказанного выше k 0Î N 0, t 0 Î N, наименьшие натуральные числа, удовлетворяющие условию (1).
Пусть теперь для чисел k Î N 0, t Î N выполняется условие (2), тогда выполняется и условие (1). НОД многочленов l k (l t -1)·d, 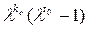 . Применяя теорему о вычислении НОД многочленов методом получим
. Применяя теорему о вычислении НОД многочленов методом получим
 ,
,
где k 1 = min(k 0, k), t 1 = НОД(t 0, t). Так как 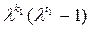 - линейная комбинация многочленов l k (l t -1)·d,
- линейная комбинация многочленов l k (l t -1)·d, 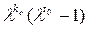 , то следует, что равенство (1) выполняется для чисел k = k 1, t = t 1. Тогда k 1 ³ t 0 или t 1 ³ t 0. Из этих неравенств следует, что k 1 = t 0 и t 1 = t 0.. Тогда k ³ k 0, t 0| t.
, то следует, что равенство (1) выполняется для чисел k = k 1, t = t 1. Тогда k 1 ³ t 0 или t 1 ³ t 0. Из этих неравенств следует, что k 1 = t 0 и t 1 = t 0.. Тогда k ³ k 0, t 0| t.
Обратно, пусть выполняются условия (3). Тогда
 .
.
Поэтому для чисел k и t выполняется условие (1). Отсюда выполняется условие (2).
Следствие 1. Если d - периодическая последовательность над полем F, то для любого многочлена g (l) Î F [l] последовательность a = g (l)·d – периодическая над полем F, причем
k (a) £ k (d),t(a)|t(d). (4)
Доказательство. Пусть k 0= k (d), t 0= t(d). Тогда
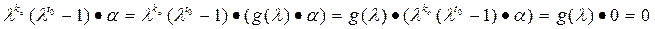 .
.
Тогда по теореме 1 k (a) £ k 0,t(a)| t 0.
Следствие 2. Если a, b - периодические последовательности над полем F, то последовательность d = a + b периодическая и
k (d) £ max{ k (a), k (b)),t(d)|НОК(t(a),t(b)). (5)
При этом:
1) если k (a) ¹ k (b), то
k (d) = max{ k (a), k (b)); (6)
2) если (t(a),t(b)) = 1, то
t(d) = НОК(t(a),t(b)); (7)
3) если a, b - ЛРП, для которых можно указать взаимно простые характеристические многочлены, то справедливы равенства (6), (7).
Доказательство. Пусть k = max{ k (a), k (b)), t = НОК(t(a),t(b)). Тогда по теореме 1  Следовательно,
Следовательно,
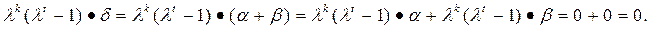
k 0= k (d), t 0= t(d). Тогда по теореме 11, получаем соотношения (4).
1) Пусть k (a) ¹ k (b), например, k (a) < k (b). Тогда k = k (b). По доказанному выше k (d) £ k. Докажем, что k (d) £ k. Допустим противное, что k (d) < k. Тогда многочлен 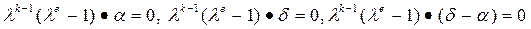 . Поэтому
. Поэтому 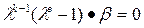 и по теореме 1 k (b)£ k – 1. Что невозможно. Следовательно, k (d) = k и формула (5) доказана.
и по теореме 1 k (b)£ k – 1. Что невозможно. Следовательно, k (d) = k и формула (5) доказана.
2) Пусть (t(a),t(b)) = 1, и t(d) = t. Далее
 .
.
Так как t |(tl), t |t(a), то по теореме 1 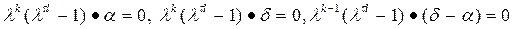 .
.
Поэтому  и по теореме 1 t (b) | t l. Так как (t (b), l) = 1, то t (b) | t. Аналогично доказывает.
и по теореме 1 t (b) | t l. Так как (t (b), l) = 1, то t (b) | t. Аналогично доказывает.
3) Пусть a, b - ЛРП, для которых можно указать взаимно простые характеристические многочлены f (l), g (l). Тогда f (l)·a= 0, g (l)·b= 0 и поэтому (f (l) g (l))·(a+b) = 0. Так как 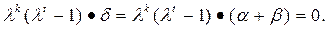
Тогда по теореме 1 k (a) £ k 0,t(a)| t 0.
разложения на неприводимые множители
Теорема 1. Любое решение d = {d x }Î s (f) линейного рекуррентного уравнения периодично, т.е. существует такое натуральное число t, что для любого x Î N 0 выполняется равенство d x + t = d x.
Доказательство. В силу теоремы 2 параграфа 3 достаточно доказать, что существуют такие натуральные числа k и l, что
d k = d l, d k + 1 = d l + 1, …, d k + n - 1 = d l + n - 1. (1)
Так как всего различных наборов вида (b 1, b 2,…, bn)над полем Fp конечно и равно pn. Поэтому, если k > l и t = k - l наименьшее число со свойством (1), то t £ pn -1.
Определение 1. Наименьший натуральный период t решения d линейного рекуррентного уравнения называется примитивным периодом решения d. Обозначаем примитивный период решения d через per d.
Теорема 2. Если F = Fp, d = {d x }Î s F (f), f Î Fp [l], то per d £ pn -1.
Доказательство. Число различных наборов (d0, d1,…, d n - 1) равно pn. Если (d0, d1,…, d n - 1) = (0, 0, …, 0), то d = {0} и per d = 1 £ pn -1.
Если (d0, d1,…, d n - 1) ¹ (0, 0,…,0), то для любого x Î N 0 набор (d x, d x +1,…,d x + n - 1) ¹ (0, 0, …, 0), а число ненулевых наборов вида (d x, d x +1,…, d x + n - 1) равно pn -1. Поэтому даже, если все они встретятся, то при некотором t имеем (d0, d1,…, d n - 1) = (d t, d t +1,…, d t + n - 1). Следовательно, per d £ pn -1.
Аннулирующие многочлены
Определение 1. Многочлен f Î F [l] называется нормированным, если его старший коэффициент равен1.
Определение 2. Многочлен g Î F [l] называется аннулирующим последовательность d, если g (l)·d= 0.
Пусть F = Fp, A F (d) = A (d) – множество всех многочленов, аннулирующих последовательность d.
Пример 1. Пусть d решение уравнения
d x + n = a 1d x + n - 1 + a 2d x + n - 2 + …+ an d x (1)
t = per d. Тогда
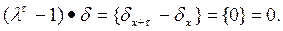
Таким образом, lt - 1 – аннулирующий многочлен решения d.
Теорема 1. Характеристический многочлен уравнения (1) аннулирует любое решение d уравнения (1).
Доказательство. Пусть d = {d x } – любое решение уравнения (1),
f (l) = l n - a 1l n- 1 - …+ an Î Fp [l]
- характеристический многочлен уравнения (1). Тогда для любого x Î N 0 имеем
f (l)·d = a = {a x },
где
a x = (Tn - a 1 T n- 1 - …+ an)·d x = a x = Tn ·d x - a 1 T n- 1·d x - …+ an d x =
= d x +n - a 1d x + n - 1-…- an d x = 0,
так как d - решение уравнения (1).
Теорема 2. Пусть d Î s – последовательность над полем Fp,
f (l) = l n - a 1l n - 1 - …+ an Î Fp [l]
- нормированный многочлен со свободным членом неравным нулю. Полиномиальный оператор f аннулирует последовательность d тогда и только тогда, когда d - решение линейного рекуррентного уравнения с характеристическим многочленом f.
Доказательство. Если d – решение уравнения (1), то по доказанному в теореме 1 полиномиальный оператор f аннулирует d.
Обратно пусть полиномиальный оператор f аннулирует d, т.е. f ·d = a = 0, т.о.
для любого x Î N 0 имеем
a x = (Tn - a 1 T n- 1 - …+ an)·d x = a x = Tn ·d x - a 1 T n- 1·d x - …+ an d x =
= d x +n - a 1d x + n - 1-…- an d x = 0.
Отсюда
d x +n = a 1d x + n - 1+…+ an d x
и d = {d x } – решение уравнения (1).
Теорема 3. Пусть d Î s (f), F = Fp; g, h Î A F (d) = A (d); q Î Fp [l]. Тогда:
1) g + h Î A F (d),
2) g - h Î A F (d),
3) gq Î A F (d).
Доказательство. Пусть g, h Î A F (d) = A (d); q Î Fp [l]. Тогда g ·d = 0, h ·d = 0. Тогда по теореме 4 параграфа 2 имеем
(g + h)·d = g ·d + h ·d = 0 + 0 = 0;
(g - h)·d = g ·d - h ·d = 0 - 0 = 0;
(gq)·d = q ·(g ·d)= q ·0 = 0.
Отсюда следует утверждение теоремы.
Определение 3. Минимальным многочленом последовательности d Î s (f) называется нормированный многочлен наименьшей степени из A (d).
Примеры. Если d = 0, то m d(l) = 1.
Если для любого x Î N 0 имеем d x +1 = d x и d x ¹ 0, то m d(l) = l -1.
d ¹ 0 тогда и только тогда, когда deg m d(l) ³ 1.
Теорема 4 (основное свойство минимального многочлена). Многочлен g Î Fp [l] принадлежит A F (d) тогда и только тогда, когда g делится на минимальный многочлен m d(l) решения d.
Доказательство. Необходимость.Пусть g Î A F (d). Докажем, что m d(l)| g. Допустим, что это не так. Тогда разделим g на m d(l) с остатком
g (l)= m d(l) q (l) + r (l),
где q (l), r (l)Î Fp [l], и deg r (l) < deg m d(l). Тогда
r (l)·d = (g (l)- m d(l) q (l))·d = g (l)·d- m d(l) q (l)·d = 0 + 0 = 0,
и r (l)Î A F (d) и deg r (l) ³ deg m d(l). Получаем противоречие.
Достаточность. Пусть m d(l)| g. Тогда g (l)= m d(l) q (l), где q (l)Î Fp [l].Тогда по теореме 4 параграфа 2 имеем
g ·d = (m d q)·d = q ·(m d·d) = q ·0 = 0.
Теорема 5. Минимальный многочлен главного решения уравнения (1) есть характеристический многочлен этого уравнения.
Доказательство. Пусть d – главное решение уравнения (1), m d(l) – минимальный многочлен d, f – характеристический многочлен уравнения (1). Так как f ·d = 0, то по теореме 4 m d(l)| f и, следовательно, deg m d(l) £ deg f. По определению главного решения последовательности d, T ·d,…, Tn - 1·d образуют базис пространства решений S (f). Так как для любого i = 1, 2,…, n -1
m d(l)·(Ti ·d) = Ti ·(m d(l)·d) = Ti ·0 = 0,
то многочлен m d(l) аннулирует любой элемент из S (f). Тогда S (f) Í S (m d). Поэтому число элементов в S (f) не меньше чем в S (m d):
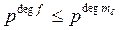 .
.
Следовательно, deg f £ deg m d(l). Отсюда deg m d(l) = deg f. Так как m d(l)| f и оба многочлена нормированные, то отсюда следует, что m d(l) = f.



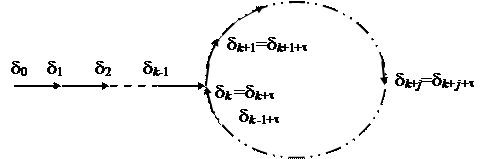
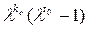 . Применяя теорему о вычислении НОД многочленов методом получим
. Применяя теорему о вычислении НОД многочленов методом получим ,
,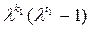 - линейная комбинация многочленов l k (l t -1)·d,
- линейная комбинация многочленов l k (l t -1)·d,  .
.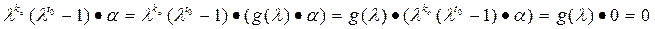 .
. Следовательно,
Следовательно,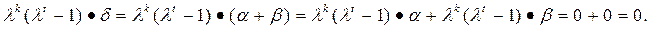
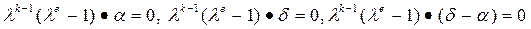 . Поэтому
. Поэтому 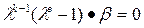 и по теореме 1 k (b)£ k – 1. Что невозможно. Следовательно, k (d) = k и формула (5) доказана.
и по теореме 1 k (b)£ k – 1. Что невозможно. Следовательно, k (d) = k и формула (5) доказана. .
.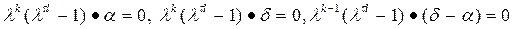 .
. и по теореме 1 t (b) | t l. Так как (t (b), l) = 1, то t (b) | t. Аналогично доказывает.
и по теореме 1 t (b) | t l. Так как (t (b), l) = 1, то t (b) | t. Аналогично доказывает.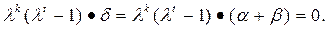
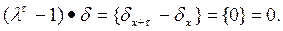
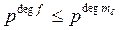 .
.


