Лекция №9
Кривые второго порядка. Окружность
 (1) – общее уравнение второй степени относительно x и y, где A, B, C, D, E, F Î R и A, B, C одновременно не равны 0.
(1) – общее уравнение второй степени относительно x и y, где A, B, C, D, E, F Î R и A, B, C одновременно не равны 0.
def. Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих декартовых координат.
Кривыми второго порядка являются: эллипс (частный случай – окружность); гипербола; парабола.
def. Окружностью называется геометрическое место точек плоскости, равноудаленных от данной точки, называемой центром.
Рассмотрим на плоскости
Oxy (в прямоугольной декартовой системе координат) окружность радиуса
R с центром в т.
C (
a;
b) и составим её уравнение.
C (a; b) – центр окружности,
M(x; y) – произвольная точка окружности,
 .
.
По определению

Þ

.
(2) – уравнение окружности с центром в т. C (a; b) и
радиусом R.
Частный случай:
 – уравнение окружности с центром в т. O (0;0) и радиусом R.
– уравнение окружности с центром в т. O (0;0) и радиусом R.
Раскроем скобки в уравнении (2):  Þ
Þ
 .
.
Обозначим  ;
;  ;
;  .
.
 – уравнение второй степени относительно x и y.
– уравнение второй степени относительно x и y.
Его особенности:  .
.
Обратно, если в (1)  , то (1) определяет окружность.
, то (1) определяет окружность.
Пример2.1. Дано уравнение  . Доказать, что это уравнение определяет окружность. Найти центр и радиус.
. Доказать, что это уравнение определяет окружность. Найти центр и радиус.
§
3.Эллипс
I. Определение эллипса. Вывод канонического уравнения.
def.
Эллипсом называется геометрическое место точек, сумма расстояния которых
до двух данных точек, называемых фокусами, есть величина постоянная.
Обозначим  – фокусы,
– фокусы,

– расстояние между фокусами.
М – производная точка эллипса.
2а – постоянная величина, равная сумме расстояний от М до  .
.
 =const=2 a (1)-
=const=2 a (1)-
по определению эллипса.
2a>2c Þ a>c.
Введем систему координат следующим образом: ось
OX проведем через фокусы

, начало координат поместим в середину отрезка

. Ось
OY проведем через середину отрезка

перпендикулярно
OX.
М (x; y) – произвольная точка эллипса,
 (c;0),
(c;0),  (– c;0) – фокусы эллипса.
(– c;0) – фокусы эллипса.

,

.Подставляя в (1), получим:
 (2) – уравнение эллипса в выбранной системе координат.
(2) – уравнение эллипса в выбранной системе координат.
Упростим данное уравнение:  .
.
Возведем обе части в квадрат:
 Þ
Þ
 .
.
Разделим обе части на (-4):  .
.
Возведем обе части в квадрат:
 Þ
Þ
 .
.
Разделим обе части на  :
:  .
.
 . Обозначим:
. Обозначим: 
 (3) – каноническое уравнение эллипса, где
(3) – каноническое уравнение эллипса, где  .
.
II. График эллипса
1. Симметрия
Из (3) получим, что эллипс имеет две оси симметрии – ось Ox и ось Oy; и центр симметрии – начало координат O (0;0).
2. Вершины эллипса
Вершины эллипса – точки пересечения эллипса с осями симметрии,
т.е. с осью
Ox и осью
Oy.

– вершины эллипса.

,

3. График эллипса  .
.
Итак,  – вершины эллипса,
– вершины эллипса,  – фокусы эллипса.
– фокусы эллипса.
def.
Отрезок

и его длина

называется
большой осью эллипса.
Отрезок

и его длина

называется
малой осью эллипса
.

–
большая полуось, 
–
малая полуось.
III. Эксцентриситет эллипса
def. Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большой оси  .
.  (4)
(4)
Поскольку  , то
, то  .
.
Выясним, как влияет величина e на форму эллипса.
 ; разделим на
; разделим на  :
:  ,
,  .
.
 , то
, то  , т.е.
, т.е.  почти равны.
почти равны.
 , то
, то  и эллипс превращается в окружность.
и эллипс превращается в окружность.
 , то
, то  , т.е.
, т.е.  , эллипс вытягивается (вдоль Ox).
, эллипс вытягивается (вдоль Ox).
Чем больше e, тем более эллипс вытянут вдоль Ox.
Планеты и кометы движутся по эллипсам. В одном из фокусов эллипса находится Солнце. Эксцентриситеты планетных орбит малы, а кометных велики ( ). Планеты движутся почти по окружности, а кометы то приближаются к Солнцу, то удаляются.
). Планеты движутся почти по окружности, а кометы то приближаются к Солнцу, то удаляются.  ;
;  ;
;  =0,97.
=0,97.
Замечание. Фокальные радиусы
 ,
,  =
=  – фокальные радиусы.
– фокальные радиусы.
Пример 3.1. Дано уравнение эллипса 16  .
.
1) Привести к каноническому виду; 2)найти длину осей;3) координаты фокусов; 4) эксцентриситет;5) построить график.
Пример 3.2. Эллипс проходит через точку M (-4;  ) и имеет
) и имеет  . Найти каноническое уравнение эллипса.
. Найти каноническое уравнение эллипса.
§ 4. Гипербола
II. График гиперболы
1. Симметрия
Гипербола имеет две оси симметрии – ось Ox и ось Oy, и центр симметрии – начало координат O (0;0).
2. Вершины. Действительные и мнимые оси
Вершины гиперболы – это точки пересечения гиперболыс осями симметрии, т.е. с осью Ox и осью Oy.
С осью Ох: у =0 






 ,
,  .
.
С осью Оу: х =0 

 нет действительных корней, гипербола не пересекается с Оу.
нет действительных корней, гипербола не пересекается с Оу.
Итак, две вершины:  и
и  .
.
def. Отрезок А 1 А 2 и его длина 2 а называется действительной осью гиперболы.
Возьмем на оси Оу две точки 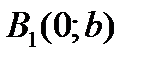 и
и  .
.
def. Отрезок В 1 В 2 и его длина 2 b называется мнимой осью гиперболы.
а – действительная полуось, b – мнимая полуось гиперболы.
3.
Асимптоты гиперболы
def. Прямая называется асимптотой кривой, если расстояние  от точки М кривой до этой прямой стремится к нулю при удалении точки М вдоль кривой в бесконечность.
от точки М кривой до этой прямой стремится к нулю при удалении точки М вдоль кривой в бесконечность.
Гипербола  имеет две асимптоты:
имеет две асимптоты:
 ,
,  – уравнение асимптот гиперболы.
– уравнение асимптот гиперболы.
4. График гиперболы  .
.
1) Построить (характеристический) прямоугольник со сторонами, параллельными осям Ох и Оу и проходящими на оси Ох на расстоянии а от точки О (0;0) по обе стороны, на оси Оу – на расстоянии b.
2) Провести асимптоты гиперболы по диагоналям прямоугольника.
3)
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAGb9ct8UA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbESPT4vCMBTE74LfITxhb5oqqKUaRQrisujBP5e9vW2e bbF5qU3U7n76jSB4HGbmN8x82ZpK3KlxpWUFw0EEgjizuuRcwem47scgnEfWWFkmBb/kYLnoduaY aPvgPd0PPhcBwi5BBYX3dSKlywoy6Aa2Jg7e2TYGfZBNLnWDjwA3lRxF0UQaLDksFFhTWlB2OdyM gq90vcP9z8jEf1W62Z5X9fX0PVbqo9euZiA8tf4dfrU/tYLpGJ5fwg+Qi38AAAD//wMAUEsBAi0A FAAGAAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54 bWxQSwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJl bHNQSwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBl eG1sLnhtbFBLAQItABQABgAIAAAAIQAZv1y3xQAAANsAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMv ZG93bnJldi54bWxQSwUGAAAAAAQABAD1AAAAigMAAAAA " filled="f" stroked="f" strokeweight=".5pt">
Вершины гиперболы в точках

и

и построить график гиперболы.
А 1, А 2– вершины гиперболы,  – фокусы гиперболы.
– фокусы гиперболы.
I. Параллельный перенос
На плоскости введена прямоугольная система координат Oxy. Перенесем точку O в точку 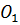 и построим новую систему координат
и построим новую систему координат 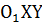 , причем
, причем 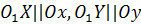 , направления осей совпадают, единицы масштаба одинаковые.
, направления осей совпадают, единицы масштаба одинаковые.
Говорят, что выполнен параллельный перенос осей координат,
причем точка 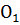 имеет координаты
имеет координаты 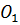 (a, b) в системе Oxy.
(a, b) в системе Oxy.
M – произвольная точка плоскости.
M (x, y) – в старой системе координат Oxy.
M (X, Y) – в новой системе координат 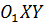 .
.
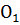 (a, b) – координаты точки
(a, b) – координаты точки 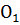 в старой системе координат.
в старой системе координат.
Справедливы формулы:
- формулы, выражающие новые координаты через старые.
- формулы, выражающие старые координаты через новые.
Эти формулы называются формулами параллельного переноса.
Замечание 1. Уравнения вида
(1)
(2)
(2)
определяют параболу с вершиной в точке 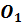 (a, b).
(a, b).
Действительно, с помощью формул параллельного переноса:
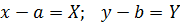 получим: (1) Þ
получим: (1) Þ 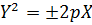 ,
,
(2) Þ 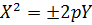 –
–
параболы с вершиной в новом начале координат 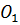 .
.
Осью симметрии параболы (1) является прямая 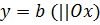 .
.
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAlYweAccA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbESPzWvCQBTE70L/h+UVetNNQ1slZhUJSEXagx8Xb8/s ywdm36bZrab9611B8DjMzG+YdN6bRpypc7VlBa+jCARxbnXNpYL9bjmcgHAeWWNjmRT8kYP57GmQ YqLthTd03vpSBAi7BBVU3reJlC6vyKAb2ZY4eIXtDPogu1LqDi8BbhoZR9GHNFhzWKiwpayi/LT9 NQrW2fIbN8fYTP6b7POrWLQ/+8O7Ui/P/WIKwlPvH+F7e6UVxOM3uJ0JR0DOrgAAAP//AwBQSwEC LQAUAAYACAAAACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNd LnhtbFBLAQItABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8u cmVsc1BLAQItABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hh cGV4bWwueG1sUEsBAi0AFAAGAAgAAAAhAJWMHgHHAAAA3AAAAA8AAAAAAAAAAAAAAAAAmAIAAGRy cy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPUAAACMAwAAAAA= " filled="f" stroked="f" strokeweight=".5pt">
Осью симметрии параболы (2) является прямая
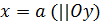
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEA/lQnQscA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbESPQWvCQBSE70L/w/IKvenGQINNXUUCoUXsweilt9fs Mwlm36bZrYn++m6h4HGYmW+Y5Xo0rbhQ7xrLCuazCARxaXXDlYLjIZ8uQDiPrLG1TAqu5GC9epgs MdV24D1dCl+JAGGXooLa+y6V0pU1GXQz2xEH72R7gz7IvpK6xyHATSvjKEqkwYbDQo0dZTWV5+LH KNhm+Qfuv2KzuLXZ2+606b6Pn89KPT2Om1cQnkZ/D/+337WCOHmBvzPhCMjVLwAAAP//AwBQSwEC LQAUAAYACAAAACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNd LnhtbFBLAQItABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8u cmVsc1BLAQItABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hh cGV4bWwueG1sUEsBAi0AFAAGAAgAAAAhAP5UJ0LHAAAA3AAAAA8AAAAAAAAAAAAAAAAAmAIAAGRy cy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPUAAACMAwAAAAA= " filled="f" stroked="f" strokeweight=".5pt">
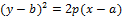
|
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEA6rcYAsMA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbERPy4rCMBTdC/MP4Q6403QKo6VjFCmIg+jCx8bdtbm2 ZZqbThO1+vVmIbg8nPdk1plaXKl1lWUFX8MIBHFudcWFgsN+MUhAOI+ssbZMCu7kYDb96E0w1fbG W7rufCFCCLsUFZTeN6mULi/JoBvahjhwZ9sa9AG2hdQt3kK4qWUcRSNpsOLQUGJDWUn53+5iFKyy xQa3p9gkjzpbrs/z5v9w/Faq/9nNf0B46vxb/HL/agXxOMwPZ8IRkNMnAAAA//8DAFBLAQItABQA BgAIAAAAIQDw94q7/QAAAOIBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1s UEsBAi0AFAAGAAgAAAAhADHdX2HSAAAAjwEAAAsAAAAAAAAAAAAAAAAALgEAAF9yZWxzLy5yZWxz UEsBAi0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABAAAAAAAAAAAAAAAAAAKQIAAGRycy9zaGFwZXht bC54bWxQSwECLQAUAAYACAAAACEA6rcYAsMAAADcAAAADwAAAAAAAAAAAAAAAACYAgAAZHJzL2Rv d25yZXYueG1sUEsFBgAAAAAEAAQA9QAAAIgDAAAAAA== " filled="f" stroked="f" strokeweight=".5pt">
.
Пример 6.1. Найти координаты вершины параболы, построить график:
а) 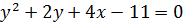 ; б)
; б) 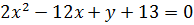 .
.
Замечание 2. Если в уравнениях эллипса и гиперболы заменить х и у соответственно на 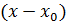 и
и 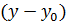 , то полученные уравнения будут определять те же линии, но со смещенным центром (вместо
, то полученные уравнения будут определять те же линии, но со смещенным центром (вместо 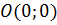 будет
будет 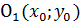 ).
).
II. Поворот осей координат
На плоскости задана прямоугольная система координат Oxy. Повернем координатные оси на угол α, не меняя начала координат. Получим новую систему координат OХУ.
М – произвольная точка плоскости,
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEA9gox78QA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbERPTWvCQBC9F/oflhF6qxsDLZK6igSCIvUQ66W3MTsm wexsml2T1F/fFYTe5vE+Z7EaTSN66lxtWcFsGoEgLqyuuVRw/Mpe5yCcR9bYWCYFv+RgtXx+WmCi 7cA59QdfihDCLkEFlfdtIqUrKjLoprYlDtzZdgZ9gF0pdYdDCDeNjKPoXRqsOTRU2FJaUXE5XI2C XZrtMT/FZn5r0s3ned3+HL/flHqZjOsPEJ5G/y9+uLc6zI9iuD8TLpDLPwAAAP//AwBQSwECLQAU AAYACAAAACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnht bFBLAQItABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8ucmVs c1BLAQItABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hhcGV4 bWwueG1sUEsBAi0AFAAGAAgAAAAhAPYKMe/EAAAA3AAAAA8AAAAAAAAAAAAAAAAAmAIAAGRycy9k b3ducmV2LnhtbFBLBQYAAAAABAAEAPUAAACJAwAAAAA= " filled="f" stroked="f" strokeweight=".5pt">
М (
x;
y) – в старой системе
координат Оху,
M (X; Y) – в новой системе
координат OXY.
Тогда 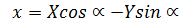 (3) –
(3) –
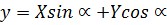
формулы поворота координатных осей.
III. Общий случай преобразования координат
Пусть на плоскости заданы две декартовы прямоугольные системы координат Oxy и O1XY с разным началом и разными направлениями осей.
О 1(а, b)-координаты О 1 в системе координат Oxy,
α – угол, который образует ось O 1 X c осью Ox.
Возьмем т. М. М (x; y) – в координатной плоскости Oxy,
M (X; Y)– в координатной плоскости O1ХУ.
Введем промежуточную систему координат O 1  , где O1
, где O1  Ox, O1
Ox, O1 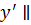 Oy.
Oy.
Переход от Oxy к O 1 XY осуществляется за два шага:
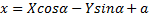
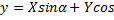 α+ b α+ b
|
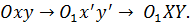
Тогда
Лекция №9
Кривые второго порядка. Окружность
 (1) – общее уравнение второй степени относительно x и y, где A, B, C, D, E, F Î R и A, B, C одновременно не равны 0.
(1) – общее уравнение второй степени относительно x и y, где A, B, C, D, E, F Î R и A, B, C одновременно не равны 0.
def. Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих декартовых координат.
Кривыми второго порядка являются: эллипс (частный случай – окружность); гипербола; парабола.
def. Окружностью называется геометрическое место точек плоскости, равноудаленных от данной точки, называемой центром.
Рассмотрим на плоскости
Oxy (в прямоугольной декартовой системе координат) окружность радиуса
R с центром в т.
C (
a;
b) и составим её уравнение.
C (a; b) – центр окружности,
M(x; y) – произвольная точка окружности,
 .
.
По определению

Þ

.
(2) – уравнение окружности с центром в т. C (a; b) и
радиусом R.
Частный случай:
 – уравнение окружности с центром в т. O (0;0) и радиусом R.
– уравнение окружности с центром в т. O (0;0) и радиусом R.
Раскроем скобки в уравнении (2):  Þ
Þ
 .
.
Обозначим  ;
;  ;
;  .
.
 – уравнение второй степени относительно x и y.
– уравнение второй степени относительно x и y.
Его особенности:  .
.
Обратно, если в (1)  , то (1) определяет окружность.
, то (1) определяет окружность.
Пример2.1. Дано уравнение  . Доказать, что это уравнение определяет окружность. Найти центр и радиус.
. Доказать, что это уравнение определяет окружность. Найти центр и радиус.
§
3.Эллипс


 (1) – общее уравнение второй степени относительно x и y, где A, B, C, D, E, F Î R и A, B, C одновременно не равны 0.
(1) – общее уравнение второй степени относительно x и y, где A, B, C, D, E, F Î R и A, B, C одновременно не равны 0. .
.
 Þ
Þ  .
.
 – уравнение окружности с центром в т. O (0;0) и радиусом R.
– уравнение окружности с центром в т. O (0;0) и радиусом R. Þ
Þ .
. ;
;  ;
;  .
. – уравнение второй степени относительно x и y.
– уравнение второй степени относительно x и y.  .
. . Доказать, что это уравнение определяет окружность. Найти центр и радиус.
. Доказать, что это уравнение определяет окружность. Найти центр и радиус.

 – фокусы,
– фокусы, – расстояние между фокусами.
– расстояние между фокусами.
 =const=2 a (1)-
=const=2 a (1)-

 , начало координат поместим в середину отрезка
, начало координат поместим в середину отрезка  . Ось OY проведем через середину отрезка
. Ось OY проведем через середину отрезка  (c;0),
(c;0),  (– c;0) – фокусы эллипса.
(– c;0) – фокусы эллипса. ,
,  .Подставляя в (1), получим:
.Подставляя в (1), получим:
 (2) – уравнение эллипса в выбранной системе координат.
(2) – уравнение эллипса в выбранной системе координат. .
. Þ
Þ .
. .
. Þ
Þ .
. :
:  .
. . Обозначим:
. Обозначим: 
 (3) – каноническое уравнение эллипса, где
(3) – каноническое уравнение эллипса, где  .
. – вершины эллипса.
– вершины эллипса. ,
, 
 – вершины эллипса,
– вершины эллипса,  – фокусы эллипса.
– фокусы эллипса.

 и его длина
и его длина  называется большой осью эллипса.
называется большой осью эллипса. и его длина
и его длина  называется малой осью эллипса .
называется малой осью эллипса . – большая полуось,
– большая полуось,  – малая полуось.
– малая полуось.
 .
.  (4)
(4) , то
, то  .
. ; разделим на
; разделим на  :
:  ,
,  .
. , то
, то  , т.е.
, т.е.  почти равны.
почти равны. , то
, то  и эллипс превращается в окружность.
и эллипс превращается в окружность. , то
, то  , т.е.
, т.е.  , эллипс вытягивается (вдоль Ox).
, эллипс вытягивается (вдоль Ox).  ;
;  ;
;  =0,97.
=0,97. ,
,  =
=  – фокальные радиусы.
– фокальные радиусы. .
. ) и имеет
) и имеет  . Найти каноническое уравнение эллипса.
. Найти каноническое уравнение эллипса.




 ,
,  .
.
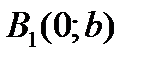 и
и  .
.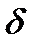
 от точки М кривой до этой прямой стремится к нулю при удалении точки М вдоль кривой в бесконечность.
от точки М кривой до этой прямой стремится к нулю при удалении точки М вдоль кривой в бесконечность. имеет две асимптоты:
имеет две асимптоты: ,
,  – уравнение асимптот гиперболы.
– уравнение асимптот гиперболы. .
. и построим новую систему координат
и построим новую систему координат  , причем
, причем 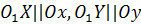 , направления осей совпадают, единицы масштаба одинаковые.
, направления осей совпадают, единицы масштаба одинаковые. имеет координаты
имеет координаты 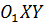 .
.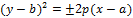
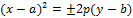
 (a, b).
(a, b).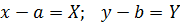 получим: (1) Þ
получим: (1) Þ 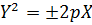 ,
,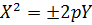 –
–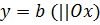 .
.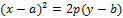
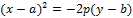
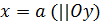
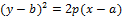
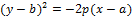
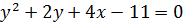 ; б)
; б) 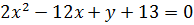 .
.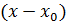 и
и 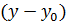 , то полученные уравнения будут определять те же линии, но со смещенным центром (вместо
, то полученные уравнения будут определять те же линии, но со смещенным центром (вместо 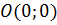 будет
будет 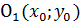 ).
).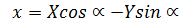 (3) –
(3) –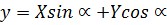
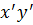 , где O1
, где O1 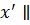 Ox, O1
Ox, O1 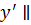 Oy.
Oy.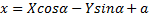
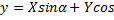 α+ b
α+ b