О.1/ функция называется примитивно рекурсивной функцией, если она может быть получена из простейшей функции 0(х), f(x)  с помощью конечного числа применений операторов суперпозиций и примитивной рекурсии.
с помощью конечного числа применений операторов суперпозиций и примитивной рекурсии.
О.2/ 1) функции 0(х), f(x)  для любых
для любых 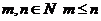 является примитивной рекурсивной функцией
является примитивной рекурсивной функцией
2) Если 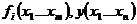 при
при  простейшая рекурсивная функция то
простейшая рекурсивная функция то 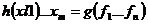 - является простейшей
- является простейшей
3) если 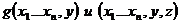 - п.р.ф. при
- п.р.ф. при  то
то  -является п.р.ф.
-является п.р.ф.
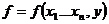
4) других п.р.ф. нет
Примеры простейших рекурсивных функций
1) все const – это п.р.ф.
0=0(х) 1=S(0(x)) 2=S(S(0(x))) m=S(S…(S(0(x)))…)
2) Сложение f(x,y)=x+y-п.р.ф.
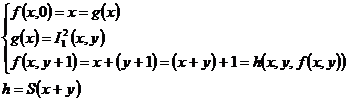
3) Умножение f(x,y)=x●y-п.р.ф.

4) Функция 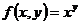 примитивная функция
примитивная функция 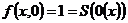
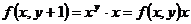 по пункту 3 умножения п.р.ф.
по пункту 3 умножения п.р.ф.
5) Функция 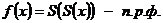
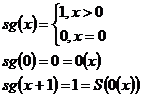
6) Функция антисигнум - 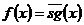 явл примитивной реу ф
явл примитивной реу ф

7) Функция вычит 1.  п.р.ф.
п.р.ф.

8) Функция усеченная разность 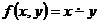 п.р.ф
п.р.ф
 из пункта 7 ф. вычитание 1 – п.р.ф.
из пункта 7 ф. вычитание 1 – п.р.ф.
9) Функция модуль разности  п.р.ф.
п.р.ф.
 т.к. функция усеч разность и сложение п.р.ф =>
т.к. функция усеч разность и сложение п.р.ф => 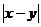 п.р.ф
п.р.ф
10) Функция  -п.р.ф
-п.р.ф

другой вариант
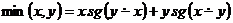
11) Функция  -п.р.ф
-п.р.ф

другой вариант
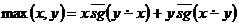
12) множество логических функций – п.р.ф

Рассмотрим множество принимающее значение 0 или 1 ({0,1})
т.к. система лог функций образует основной логический базис (из-за того что для любой лог ф. можно получить формулу в виде СДНД или СКНД каждая из которых содержит указанные функции.
то из (*) => приметив рекурс всех логических функций.
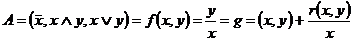
g – целая часть
r – остаток
не определена при x=0

13) Остаток от деления п.р.ф
 является п.р.ф т.к. пункты 2,3,5,9 – п.р.ф.
является п.р.ф т.к. пункты 2,3,5,9 – п.р.ф.
14) Целая часть от деления
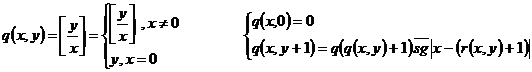
15) Функция делимости – п.р.ф.
div(x,y)

16) функция отличная от нуля в конечном числе точек – п.р.ф.

Вывод: из простейших функций 0(x) S(x)  с помощью операторов суперпозиции и примитив функций можно получить огромное разнообразие функций включая основные функции арифметической алгебры с поправкой на целочисленность. Эти функции имеют п.р. описание которое однозначно определяет процедуру их вычисления => они относятся к классу вычисляемых ф. Вычисемые п.р.ф. всюду определены это => из того что простейшие ф. всюду определены а оператор суперпозиции и примитивная рекурсия это свойство сохраняет.
с помощью операторов суперпозиции и примитив функций можно получить огромное разнообразие функций включая основные функции арифметической алгебры с поправкой на целочисленность. Эти функции имеют п.р. описание которое однозначно определяет процедуру их вычисления => они относятся к классу вычисляемых ф. Вычисемые п.р.ф. всюду определены это => из того что простейшие ф. всюду определены а оператор суперпозиции и примитивная рекурсия это свойство сохраняет.
Оператор минимизации.
( - оператор)
- оператор)
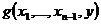 n- местная частная функция набор переменных
n- местная частная функция набор переменных 
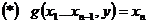
Решая (*) относит y последовательно вычисляя  наименьшим значением y при котором выясняется (*) обозначим через
наименьшим значением y при котором выясняется (*) обозначим через 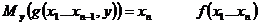 о которой говоря что она получается из функции g применением оператора минимизации.
о которой говоря что она получается из функции g применением оператора минимизации. 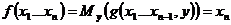
К определению оператора минимизации значение 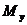 не определимо в следующих случаях:
не определимо в следующих случаях:
1. Если в процессе вычисления встретилось некоторое y при котором знач  не определенно а при всех
не определенно а при всех 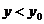 равенство (*) не выполняется.
равенство (*) не выполняется.
2. Значение  определено при любых y отличных от xn
определено при любых y отличных от xn
Вывод: Используя оператор минимизации мы имеем всюдуопред. можем получить не всюду определенную(частичную) функцию.
Частно рекурсивные функции
Функция 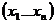 частно рекурсивная ели она может быть получена из простейших функций применением конечного числа операторов суперпозиций.
частно рекурсивная ели она может быть получена из простейших функций применением конечного числа операторов суперпозиций.
Замечание: Ранее на примерах показано что оператор минимизации может не привести к результату это произойдет в том случае когда на данном наборе уров. (*)  Не имеет решения в таком случае
Не имеет решения в таком случае 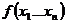 считается не определенной так среди рекурсивных функций появляются не полностью опред(частичные) функции.
считается не определенной так среди рекурсивных функций появляются не полностью опред(частичные) функции.
Частично рекурсивные функции назыв R (общерекурсивной) если она всюду определена.





 с помощью конечного числа применений операторов суперпозиций и примитивной рекурсии.
с помощью конечного числа применений операторов суперпозиций и примитивной рекурсии.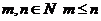 является примитивной рекурсивной функцией
является примитивной рекурсивной функцией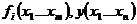 при
при  простейшая рекурсивная функция то
простейшая рекурсивная функция то 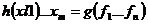 - является простейшей
- является простейшей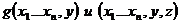 - п.р.ф. при
- п.р.ф. при  то
то  -является п.р.ф.
-является п.р.ф.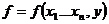
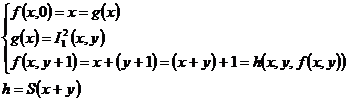

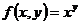 примитивная функция
примитивная функция 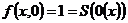
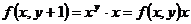 по пункту 3 умножения п.р.ф.
по пункту 3 умножения п.р.ф.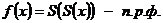
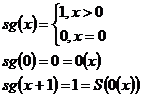
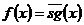 явл примитивной реу ф
явл примитивной реу ф
 п.р.ф.
п.р.ф.
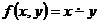 п.р.ф
п.р.ф из пункта 7 ф. вычитание 1 – п.р.ф.
из пункта 7 ф. вычитание 1 – п.р.ф. п.р.ф.
п.р.ф. т.к. функция усеч разность и сложение п.р.ф =>
т.к. функция усеч разность и сложение п.р.ф => 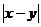 п.р.ф
п.р.ф -п.р.ф
-п.р.ф
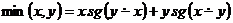
 -п.р.ф
-п.р.ф
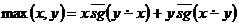

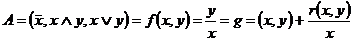

 является п.р.ф т.к. пункты 2,3,5,9 – п.р.ф.
является п.р.ф т.к. пункты 2,3,5,9 – п.р.ф.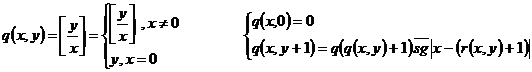


 с помощью операторов суперпозиции и примитив функций можно получить огромное разнообразие функций включая основные функции арифметической алгебры с поправкой на целочисленность. Эти функции имеют п.р. описание которое однозначно определяет процедуру их вычисления => они относятся к классу вычисляемых ф. Вычисемые п.р.ф. всюду определены это => из того что простейшие ф. всюду определены а оператор суперпозиции и примитивная рекурсия это свойство сохраняет.
с помощью операторов суперпозиции и примитив функций можно получить огромное разнообразие функций включая основные функции арифметической алгебры с поправкой на целочисленность. Эти функции имеют п.р. описание которое однозначно определяет процедуру их вычисления => они относятся к классу вычисляемых ф. Вычисемые п.р.ф. всюду определены это => из того что простейшие ф. всюду определены а оператор суперпозиции и примитивная рекурсия это свойство сохраняет. - оператор)
- оператор)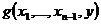 n- местная частная функция набор переменных
n- местная частная функция набор переменных 
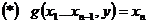
 наименьшим значением y при котором выясняется (*) обозначим через
наименьшим значением y при котором выясняется (*) обозначим через 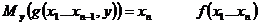 о которой говоря что она получается из функции g применением оператора минимизации.
о которой говоря что она получается из функции g применением оператора минимизации. 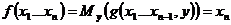
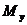 не определимо в следующих случаях:
не определимо в следующих случаях: не определенно а при всех
не определенно а при всех 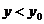 равенство (*) не выполняется.
равенство (*) не выполняется. определено при любых y отличных от xn
определено при любых y отличных от xn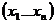 частно рекурсивная ели она может быть получена из простейших функций применением конечного числа операторов суперпозиций.
частно рекурсивная ели она может быть получена из простейших функций применением конечного числа операторов суперпозиций. Не имеет решения в таком случае
Не имеет решения в таком случае 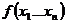 считается не определенной так среди рекурсивных функций появляются не полностью опред(частичные) функции.
считается не определенной так среди рекурсивных функций появляются не полностью опред(частичные) функции.


