

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...
Топ:
Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда...
Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров...
Основы обеспечения единства измерений: Обеспечение единства измерений - деятельность метрологических служб, направленная на достижение...
Интересное:
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
 S = a2
S = a2
Формула площади прямоугольника
Площадь прямоугольника равна произведению длин двух его смежных сторон S = a · b
где S - Площадь прямоугольника,
a, b - длины сторон прямоугольника.
Формулы площади трапеции
 Площадь трапеции равна произведению полусуммы ее оснований на высоту
Площадь трапеции равна произведению полусуммы ее оснований на высоту
| S = | (a + b) · h | |
где S - Площадь трапеции,
a, b - длины основ трапеции,
c, d - длины боковых сторон трапеции,
Билет № 6. Вопрос 1.

Корнем квадратного уравнения ax2+bx+c=0 называют всякое значение переменной x, при котором квадратный трехчлен ax2+bx+c обращается в нуль; такое значение переменной x называют также корнем квадратного трёхчлена.
Можно сказать и так: корень квадратного уравнения ax2+bx+c=0 — это такое значение x, подстановка которого в уравнение обращает уравнение в верное числовое равенство 0=0.
Решить квадратное уравнение — значит найти все его корни или установить, что корней нет.
Алгоритм решения неполных квадратных уравнений.

Примеры
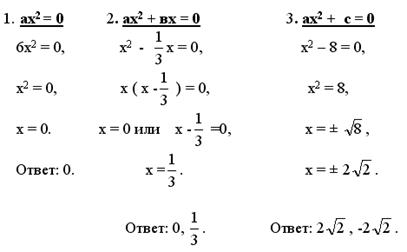
Билет № 6. Вопрос 2.
 Треугольник называется прямоугольным, если один из его углов - прямой.
Треугольник называется прямоугольным, если один из его углов - прямой.
 В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов c2=a2+b2.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов c2=a2+b2.
Известны очень многие доказательства теоремы с разными математическими методами, но одни из самых наглядных связаны с площадями.
1. Построим квадрат, сторона которого равна сумме катетов данного треугольника a+b. Площадь квадрата равна 2  (a+b):
(a+b):
 2. Если провести гипотенузы c, очевидно, что они образовали квадрат внутри построенного квадрата.
2. Если провести гипотенузы c, очевидно, что они образовали квадрат внутри построенного квадрата.
 Стороны четырёхугольника равны c, а углы — прямые, так как острые углы прямоугольного треугольника в сумме дают 90°, то угол четырёхугольника также равен 90°, потому что вместе все три угла дают 180°.
Стороны четырёхугольника равны c, а углы — прямые, так как острые углы прямоугольного треугольника в сумме дают 90°, то угол четырёхугольника также равен 90°, потому что вместе все три угла дают 180°.
|
|
Следовательно, площадь квадрата состоит из четырёх площадей равных прямоугольных треугольников 4⋅  =2ab и площади квадрата c2, образованного гипотенузами: S=c2+2аb
=2ab и площади квадрата c2, образованного гипотенузами: S=c2+2аb
3. На двух сторонах квадрата поменяем местами отрезки a и b, при этом длина стороны квадрата не меняется.
Теперь площадь квадрата можем сложить из двух площадей квадратов, образованных катетами a и b a2+b2 и двух площадей прямоугольников аb + аb: S=a2+b2+2ab
4. Из этого следуют выводы: S=c2+2аb и S=a2+b2+2ab
Площадь четырех треугольников составляет и c2=a2+b2, что и является одним из доказательств теоремы Пифагора.
Обрати внимание!
Обратная теорема используется как признак прямоугольного треугольника.
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник является прямоугольным.
Пример:
- Является ли треугольник со сторонами 6 см, 7 см и 9 см прямоугольным?
Выбираем большую сторону и проверяем, выполняется ли теорема Пифагора:
92=62+72;81≠36+49, значит, этот треугольник не прямоугольный.
- Является ли треугольник со сторонами 5 см, 12 см и 13 см прямоугольным?
Выбираем большую сторону и проверяем, выполняется ли теорема Пифагора:
132=122+52;169=144+25, значит, этот треугольник прямоугольный.
 Билет № 7. Вопрос 1.
Билет № 7. Вопрос 1.
Для построения графика функции  дадим, как обычно, независимой переменной х несколько конкретных значений (неотрицательных, поскольку при х < 0 выражение
дадим, как обычно, независимой переменной х несколько конкретных значений (неотрицательных, поскольку при х < 0 выражение  не имеет смысла) и вычислим соответствующие значения зависимой переменной у. Разумеется, мы будем давать х такие значения, для которых известно точное значение квадратного корня.
не имеет смысла) и вычислим соответствующие значения зависимой переменной у. Разумеется, мы будем давать х такие значения, для которых известно точное значение квадратного корня.
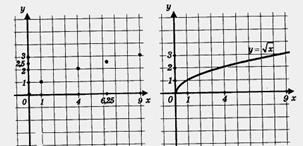
Итак, мы составили таблицу значений функции:
| x | 6,25 | ||||
| y | 2,5 |
Построим найденные точки (0; 0), (1;1), (4; 2), (6,25; 2,5), (0;3) на координатной плоскости. Они располагаются некоторой линии, начертим ее. Получили график функции  . Обратите внимание: график касается оси у в точке (0; 0). Заметим, что, имея шаблон параболы у = х2, можно без труда с его помощью построить график функции
. Обратите внимание: график касается оси у в точке (0; 0). Заметим, что, имея шаблон параболы у = х2, можно без труда с его помощью построить график функции  , ведь это — ветвь той же параболы, только ориентированная не вверх, а вправо.
, ведь это — ветвь той же параболы, только ориентированная не вверх, а вправо.
|
|
 Свойства функции
Свойства функции 
Описывая свойства этой функции, мы, как обычно, будем опираться на ее геометрическую модель — ветвь параболы (на рисунок).
1. Область определения функции — луч [0, +оо).
2. у = 0 при х = 0; поэтому начало координат принадлежит графику функции.
3. у > 0 при х > 0, график расположен в первой координатной четверти
4. Большему значению аргумента, соответствует большее значение функции, чем больше х, тем больше у.
5. Функция ограничена снизу, но не ограничена сверху. Т.к. вообще, какое бы положительное число ни взять, всегда найдется такое х, что будет выполняться неравенство  > m
> m
Функция 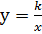 , ее свойства и график
, ее свойства и график
Коэффициент k может принимать любые значения, кроме k=0. Рассмотрим сначала случай, когда k=1; таким образом, сначала речь пойдёт о функции y= 
Чтобы построить график функции y=  , дадим независимой переменной x несколько конкретных значений и вычислим (по формулe y=
, дадим независимой переменной x несколько конкретных значений и вычислим (по формулe y=  ) соответствующие значения зависимой переменной y. Правда, на этот раз удобнее проводить вычисления и построения постепенно, сначала придавая аргументу только положительные значения, а затем — только отрицательные.
) соответствующие значения зависимой переменной y. Правда, на этот раз удобнее проводить вычисления и построения постепенно, сначала придавая аргументу только положительные значения, а затем — только отрицательные.
Первый этап. Если x=1, то y=1 (напомним, что мы пользуемся формулой y=  );
);


Второй этап. Рассмотрим отрицательные значения



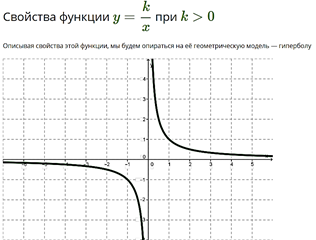
1. Область определения функции состоит из всех чисел, кроме x=0.
2. y>0 при x>0; y<0 при x<0.
3. Функция убывает на промежутках (−∞;0) и (0;+∞);
4. Функция не ограничена ни снизу, ни сверху.
5. Функция непрерывна на промежутках (−∞;0) и (0;+∞) и претерпевает разрыв при x=0.
6. Область значений функции — объединение двух открытых лучей (−∞;0)∪(0;+∞).
1. Область определения функции состоит из всех чисел, кроме x=0.
2. y>0 при x<0; y<0 при x>0.
3. Функция возрастает на промежутках (−∞;0) и (0;+∞);
4. Функция не ограничена ни снизу, ни сверху.
5. Функция непрерывна на промежутках (−∞;0) и (0;+∞) и претерпевает разрыв при x=0.
6. Область значений функции — объединение двух открытых лучей (−∞;0)∪(0;+∞).
Билет № 7. Вопрос 2.

 Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.
Коэффициентом подобия называют число k, равное отношению сходственных сторон подобных треугольников.
|
|
Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.
 Признаки подобия треугольников
Признаки подобия треугольников
|
|
|

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!