Доказательство: Проведем диагональ АС. АС – общая;
ВС = АD (по условию);
ÐВСА = ÐСАD (внутренние накрест лежащие при АD II BC и секущей АС);
Þ DАВС = DАDС (по 1 признаку).
ÐВAC = ÐACD (внутренние накрест лежащие) Þ АВ II СD.
АВСD – параллелограмм.
Признак 2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник - параллелограмм.
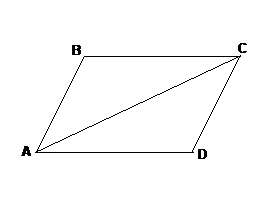 Дано: ABCD – четырехугольник; АВ = СD,
Дано: ABCD – четырехугольник; АВ = СD,
АD = BC.
Доказать: АВСD – параллелограмм.
Доказательство: Проведем диагональ АС. АС – общая;
ВС = АD (по условию);
АВ = СD (по условию);
Þ DАВС = DАDС (по 3 признаку).
ÐВСА = ÐСАD (внутренние накрест лежащие) Þ АD II BC;
ÐВAC = ÐACD (внутренние накрест лежащие) Þ АВ II СD.
АВСD – параллелограмм.
Признак 3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник - параллелограмм.
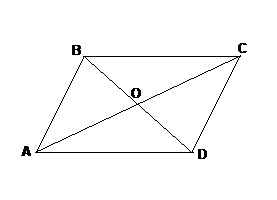 Дано: ABCD – четырехугольник;
Дано: ABCD – четырехугольник;
АС∩ВD = {О}; BO = OD; AO = OC.
Доказать: АВСD – параллелограмм.
Доказательство:
ВO = OD (по условию);
АO = OС (по условию);
ÐAOВ = ÐСOD (вертикальные);
Þ DАОВ = DDОС (по 1 признаку).
ÐОВА = ÐСDО (внутренние накрест лежащие) Þ АВ II СD;
ВO = OD (по условию);
АO = OС (по условию);
ÐСOВ = ÐАOD (вертикальные);
Þ DСОВ = DDОА (по 1 признаку).
ÐВCО = ÐОAD (внутренние накрест лежащие) Þ АD II BC.
АВСD – параллелограмм.
Ромб как частный вид параллелограмма. Свойства ромба. Признаки ромба.
Определение 1. Ромбом называется параллелограмм, все стороны которого равны.
Так как ромб является параллелограммом, то он обладает всеми свойствами параллелограмма.
Особое свойство ромба. Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
 Дано: ABCD – ромб.
Дано: ABCD – ромб.
Доказать: АС ^ ВD; ÐВАС = ÐСАD;
ÐAВD = ÐDBC.
Доказательство:
Рассмотрим DАВС.
АВ = ВС, АО = ОС.
Þ ВО – высота и биссектриса ÐАВC.
Þ ВС ^ AD; ÐАВO = ÐCВO.
Рассмотрим DАВD.
АВ = AD, BО = ОD.
Þ AО – высота и биссектриса ÐBАD.
Þ ÐВAO = ÐOAD.
Признаки ромба.
Признак 1. Если диагонали параллелограмма взаимно перпендикулярны, то параллелограмм является ромбом.
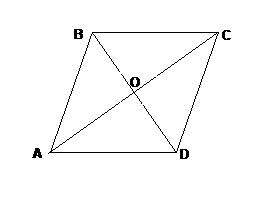 Дано: ABCD – параллелограмм; АС ^ ВD.
Дано: ABCD – параллелограмм; АС ^ ВD.
Доказать: АВСD – ромб.
Доказательство:
АО = ОС (по свойству диагоналей параллелограмма);
ВО = ОD (по свойству диагоналей параллелограмма);
ÐАОВ = ÐВОС = ÐСОD = ÐАОD = 90°;
Þ DАОВ = DВОС = DСОD = DAOD (как прямоугольные по двум катетам);
Þ АВ = ВС = СD = AD;
Þ АВСD – ромб.
Признак 2. Если диагональ параллелограмма является биссектрисой его угла, то параллелограмм является ромбом.
 Дано: ABCD – параллелограмм;
Дано: ABCD – параллелограмм;
ÐВАО = ÐОАD.
Доказать: АВСD – ромб.
Доказательство:
АО – общая;
ВО = ОD (по свойству диагоналей параллелограмма);
ÐВАО = ÐDAО (по условию);
Þ DАОВ = DAOD (как прямоугольные по катету и прилежащему острому углу);
Þ АВ = AD Þ АВСD – ромб.
Прямоугольник как частный вид параллелограмма. Свойства прямоугольника. Признак прямоугольника.
Определение 1. Прямоугольником называется параллелограмм, у которого все углы прямые.



 Дано: ABCD – четырехугольник; АВ = СD,
Дано: ABCD – четырехугольник; АВ = СD, Дано: ABCD – четырехугольник;
Дано: ABCD – четырехугольник; Дано: ABCD – ромб.
Дано: ABCD – ромб. Дано: ABCD – параллелограмм; АС ^ ВD.
Дано: ABCD – параллелограмм; АС ^ ВD.


