Уравнения Максвелла (2) образуют систему взаимосвязанных дифференциальных уравнений первого порядка, решение которой с учетом граничных условий в некоторых случаях затруднительно. Для преодоления возникающих трудностей можно воспользоваться волновыми уравнениями, являющимися следствием системы уравнений (2). Упрощения в этом случае получаются за счет того, что имеются разделяющиеся переменные и более простая форма зависимости волнового процесса от свойств среды. Для гармонических колебаний, применяя к обеим частям первого уравнения из системы (2) операцию rot, получим:
 , где
, где  .
.
Отсюда в соответствии со вторым уравнением (2) получим
 . (3)
. (3)
Используя соотношение
 , (4)
, (4)
где  – оператор Лапласа и вводя обозначение
– оператор Лапласа и вводя обозначение
 . (5)
. (5)
и подставляя (4) в (3) с учетом, что div  = 0, получим
= 0, получим
 (6)
(6)
Величина коэффициента, обозначенного через k зависит от электрических постоянных среды, в которой распространяются электромагнитные колебания, и называется коэффициентом распространения в среде. Коэффициент k в общем случае является комплексной величиной, ее действительная часть  характеризует затухание комплексных амплитуд
характеризует затухание комплексных амплитуд  и поэтому называется коэффициентом затухания, а величина
и поэтому называется коэффициентом затухания, а величина  , характеризующая фазу (задержку во времени), носит название коэффициента фазы.
, характеризующая фазу (задержку во времени), носит название коэффициента фазы.
Уравнение (6) устанавливает закон изменения вектора напряженности магнитного поля. Аналогично поступая со вторым уравнением системы (2), получим закон изменения вектора напряженности электрического поля
 (7)
(7)
Уравнения (6) и (7) дают одинаковый закон изменения соответственно векторов  и называются волновыми уравнениями в векторной форме.
и называются волновыми уравнениями в векторной форме.
Преимуществом записи волновых уравнений в векторной форме является независимость от системы координат. При решении конкретных, практических задач векторные уравнения должны быть преобразованы в систему координат, удобную для решения этих задач. Таким образом, при решении задач о распространении электромагнитных волн в однородной среде можно исходить из волнового уравнения (6) или (7) для одного из векторов поля. Определив, например  , удовлетворяющий уравнению (7), можно найти
, удовлетворяющий уравнению (7), можно найти 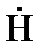 из второго уравнения системы (2) по формуле:
из второго уравнения системы (2) по формуле:

5. Плоские однородные волны как простейший случай волнового процесса
Частные решения волновых уравнений (6) и (7) приводят к понятию плоской однородной гармонической волны как простейшего случая волнового процесса. Фронтом волны называется поверхность, проходящая через точки с одинаковыми фазами. Плоской называется волна, у которой фронт – плоская поверхность.
Среда называется однородной, если ее макроскопические параметры  не зависят от координат точек пространства. Примером однородной среды является диэлектрик. Волна называется плоской и однородной, если ее гармонические векторы зависят только от одной координаты, при этом в электромагнитном поле можно провести ряд параллельных плоскостей, перпендикулярных направлению распространения волны так, чтобы векторы напряженности
не зависят от координат точек пространства. Примером однородной среды является диэлектрик. Волна называется плоской и однородной, если ее гармонические векторы зависят только от одной координаты, при этом в электромагнитном поле можно провести ряд параллельных плоскостей, перпендикулярных направлению распространения волны так, чтобы векторы напряженности  в каждый момент времени лежали в этих плоскостях и сохраняли как свое значение, так и направление вдоль всей плоскости. Основным свойством плоской волны является взаимная перпендикулярность векторов
в каждый момент времени лежали в этих плоскостях и сохраняли как свое значение, так и направление вдоль всей плоскости. Основным свойством плоской волны является взаимная перпендикулярность векторов  . Понятие плоской волны при изучении процессов распространения электромагнитных волн имеет такое же значение, как и гармонические колебания при изучении изменяющихся во времени сигналов любой формы.
. Понятие плоской волны при изучении процессов распространения электромагнитных волн имеет такое же значение, как и гармонические колебания при изучении изменяющихся во времени сигналов любой формы.
Так как волновые уравнения линейны, то общее решение уравнения является суперпозицией всех видов плоских волн, распространяющихся в любых направлениях. С учетом координатного выражения оператора Лапласа

уравнения (6) и (7) в декартовых координатах примут вид
 , (8)
, (8)
где через  обозначена комплексная амплитуда
обозначена комплексная амплитуда  .
.
Каждому уравнению вида (8) соответствует группа из трех отдельных скалярных уравнений для составляющих поля Фх, Фу, Фz.
При плоской однородной волне, распространяющейся вдоль оси z, с учетом того, что
 уравнение (8) приобретает вид
уравнение (8) приобретает вид
 (9)
(9)
где через Ф обозначена проекция вектора  на ось Х или У.
на ось Х или У.
Общее решение уравнения (9), зависящее только от координаты z, определяется выражением
 (10)
(10)
где А1 и А2 – постоянные интегрирования.
Оба слагаемых в уравнении (10) представляют плоские волны: одну бегущую (падающая волна) в направлении положительной оси z (выражение  ), другую в обратном направлении – отраженная волна (
), другую в обратном направлении – отраженная волна ( ), что обусловлено выбором временного множителя в виде
), что обусловлено выбором временного множителя в виде  .
.
5. Распространение плоских волн в диэлектрике и проводнике
При рассмотрении процессов распространения электромагнитной волны обычно приходится сталкиваться с двумя категориями материальных сред, физические свойства которых резко отличаются друг от друга. Это диэлектрические (изолирующие) среды или же металлические (проводящие) среды. Принято среду считать диэлектриком, если  и при
и при  - проводником. Некоторые среды (почва, вода) в диапазоне нижних частот обнаруживают проводниковые свойства, а выше – изолирующие.
- проводником. Некоторые среды (почва, вода) в диапазоне нижних частот обнаруживают проводниковые свойства, а выше – изолирующие.
Так как волновое уравнение для плоских волн (9) аналогично уравнению однородной линии, то имеется полная аналогия как в физических процессах, так и в используемой терминологии (коэффициент распространения волны, волновое сопротивление, коэффициент отражения).
Для идеального диэлектрика коэффициент распространения волны, согласно выражению (5), равен
 (11)
(11)
Откуда следует, что коэффициент затухания  , а коэффициент фазы
, а коэффициент фазы  .
.
Таким образом, в отношении процесса распространения электромагнитных волн однородная среда без потерь (σ=0) является прозрачной, так как не вносит затухания. Воздушная среда мало отличается от вакуума, поэтому она наиболее совершенна с точки зрения распространения в ней электромагнитных колебаний. По этой причине при конструировании кабелей связи увеличивают долю воздушных включений в изоляции жил.
В однородном диэлектрике без потерь электромагнитная волна распространяется со скоростью
 (12)
(12)
Для вакуума  , т.е. совпадает со скоростью света.
, т.е. совпадает со скоростью света.
Волновое сопротивление среды без потерь чисто реальная величина  , поэтому в любой точке поля плоской волны в вакууме отношение напряженности электрического поля к напряженности магнитного поля постоянно и равно
, поэтому в любой точке поля плоской волны в вакууме отношение напряженности электрического поля к напряженности магнитного поля постоянно и равно  .
.
Для проводника коэффициент распространения волны согласно выражению (5)
 .
.
Заменяя в подкоренном выражении величину j на 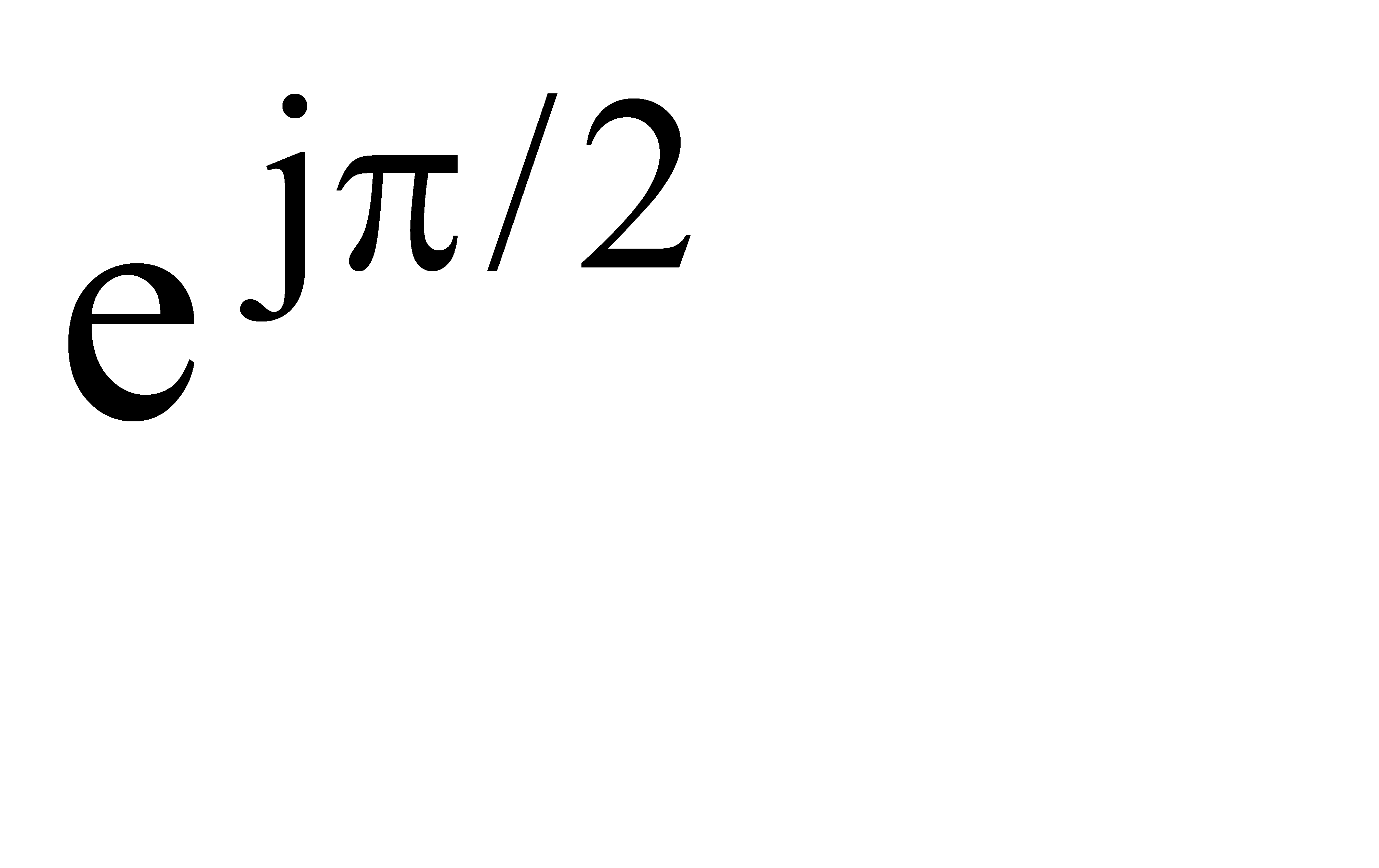 , получим что коэффициент затухания равен коэффициенту фазы
, получим что коэффициент затухания равен коэффициенту фазы
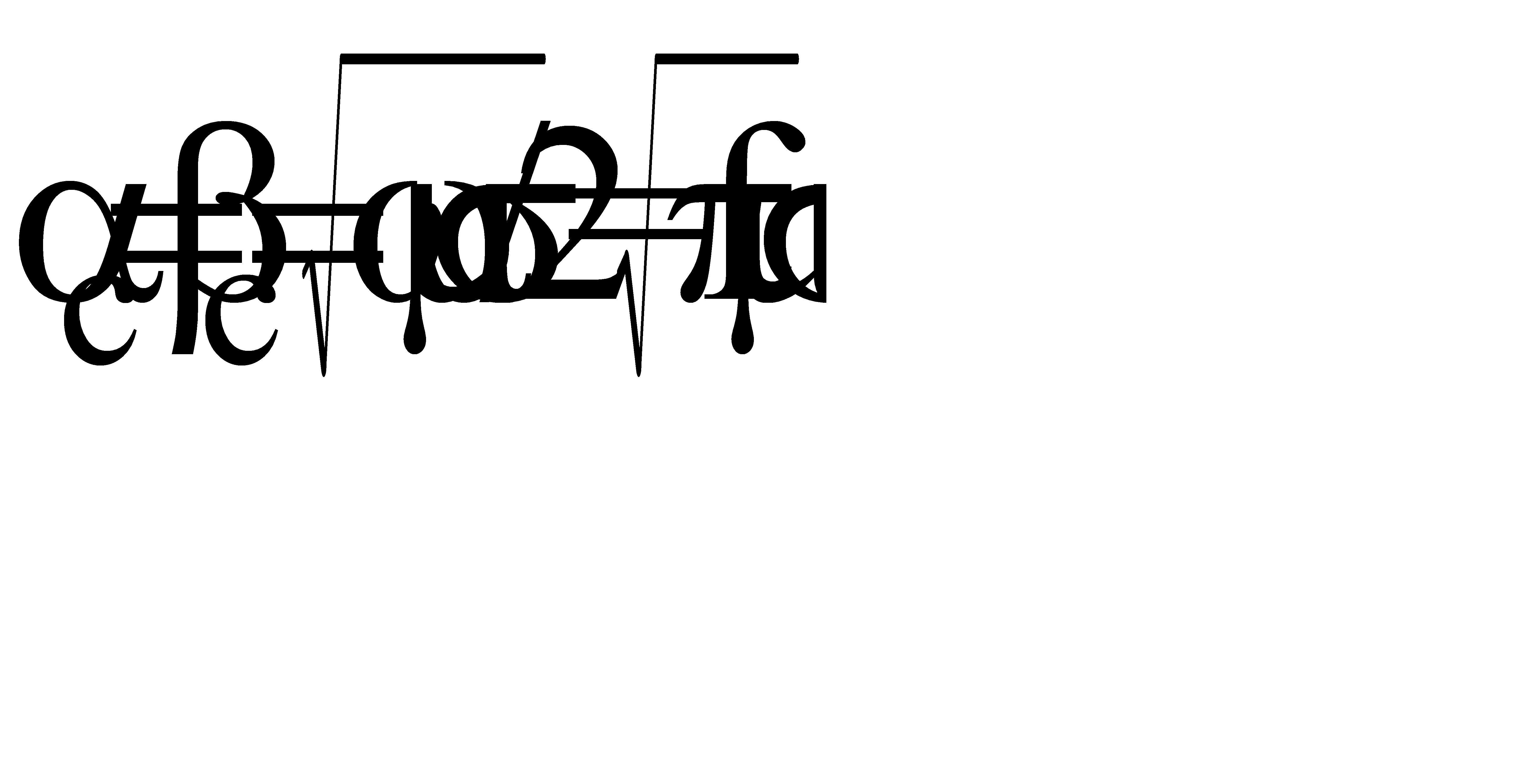 . (13)
. (13)
Следовательно электромагнитная плоская волна, попадая в металл, быстро затухает.
Из уравнения распространения волны (10) следует, что затухание волны определяется выражением  . Если задаться уменьшением напряженности поля в е = 2,71 раза на глубине
. Если задаться уменьшением напряженности поля в е = 2,71 раза на глубине  от поверхности проводника, то эта глубина определится из условия
от поверхности проводника, то эта глубина определится из условия 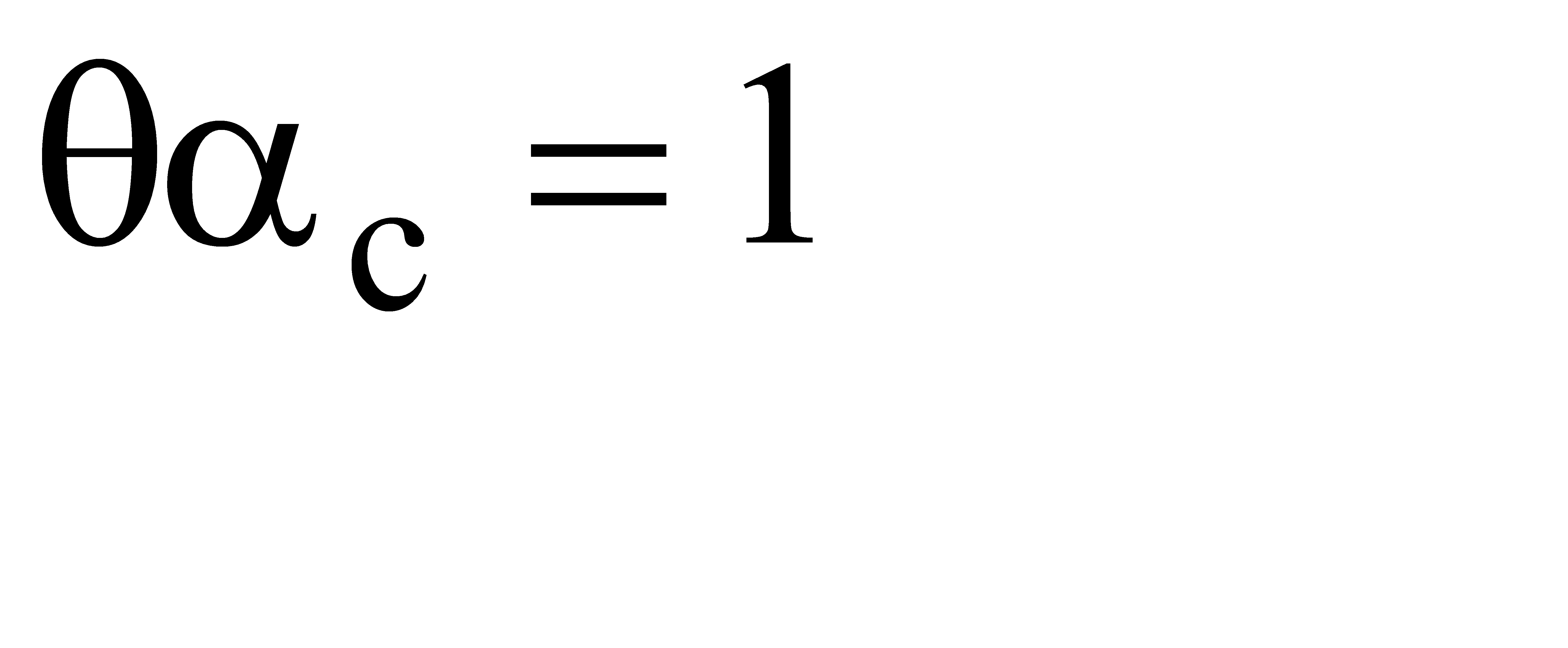 . Тогда
. Тогда  . Параметр
. Параметр  принято называть эквивалентной глубиной проникновения поля.
принято называть эквивалентной глубиной проникновения поля.
В табл.1 приведены электрические характеристики некоторых металлов и выражения для расчетов эквивалентной глубины  .
.
Таблица 1.
| Металл
| σ, См . м / мм2
| ρ, Ом . мм2/м
| 
|  ,мм ,мм
|
| Медь
|
| 0,0175
|
| 66,7/ 
|
| Алюминий
| 34,36
| 0,0292
|
| 86,4/ 
|
| Сталь
| 7,23
| 0,138
|
| 18,7/ 
|
| Свинец
| 4,52
| 0,221
|
| 236,7/ 
|
Из таблицы видно, что наибольшей глубиной проникновения поля (тока) обладает свинец.
Волновым сопротивлением среды в данной точке пространства называется комплексная величина, определяемая отношением комплексных амплитуд напряженности электрического ( ) и магнитного (
) и магнитного ( ) полей в данной точке пространства. Z
) полей в данной точке пространства. Z
 , (14)
, (14)
Волновое сопротивление проводящих сред весьма мало по сравнению с волновым сопротивлением большинства диэлектриков. Это говорит о малом значении отношения напряженностей электрического и магнитного полей в проводниках, определяемом выражением (14).
Скорость распространения гармонически колебаний в проводящей среде
 , (15)
, (15)
так же, как и волновое сопротивление, зависит от частоты, что приводит к дисперсии передаваемого сигнала. В этом заключается существенное отличие проводящих сред от вакуума и диэлектриков, обладающих независимостью диэлектрической проницаемости от частоты. Дисперсия приводит к уширению (размыванию) передаваемых импульсных сигналов и, как следствие, ограничению скорости и дальности связи.
6. Волновые уравнения в цилиндрической системе координат
Векторные уравнения (6) и (7) справедливы для любой системы координат. Для изучения распространения электромагнитной волны по направляющей системе удобно выбрать систему координат так, чтобы она соответствовала геометрии изучаемого объекта. Это имеет целью упростить формулировку граничных условий.
Для круглого сечения проводов или волноводов целесообразно выбрать цилиндрическую систему координат r, φ и z так, чтобы ось z, была направлена вдоль оси направляющей системы.
В уравнения (6) и (7) входят векторные величины, поэтому каждое из них соответствует группе из трех отдельных уравнений для составляющих векторов 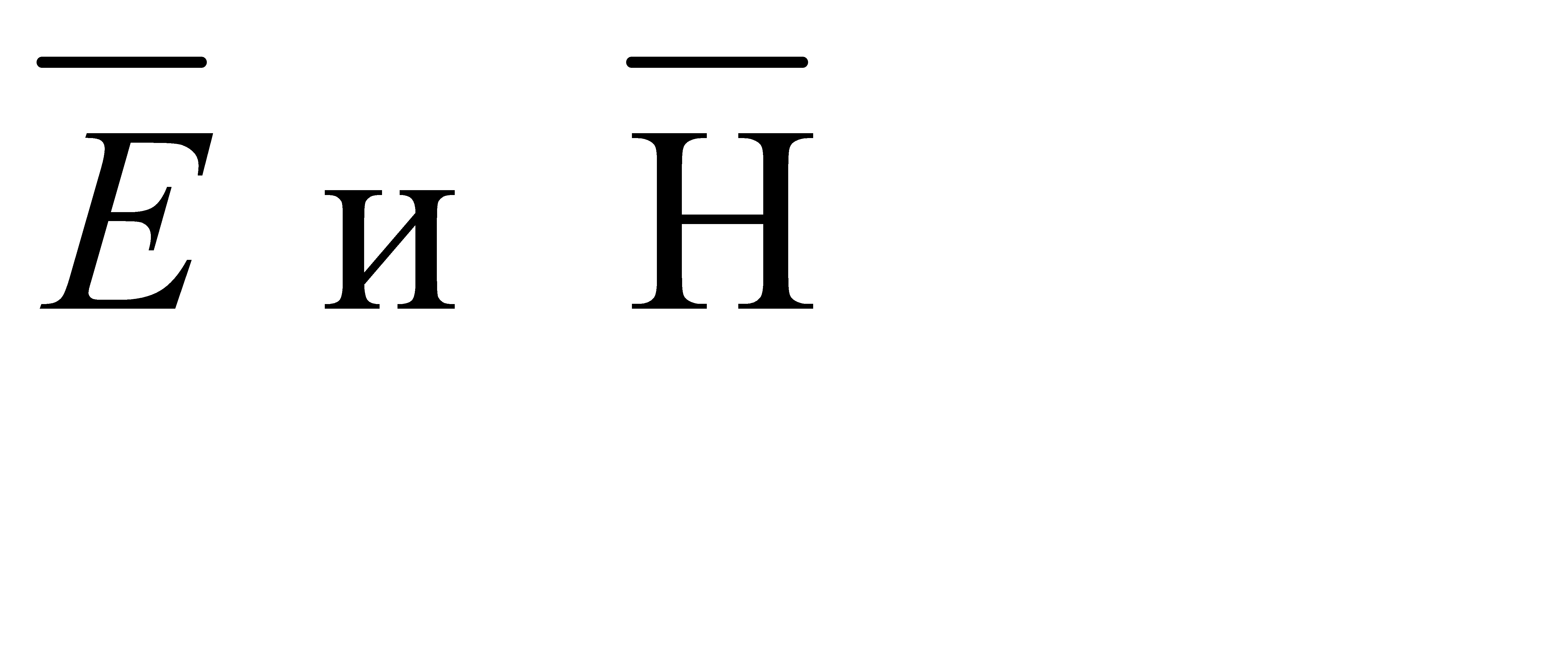 . Используемые в дальнейшем обозначения составляющих (Е r ,
. Используемые в дальнейшем обозначения составляющих (Е r ,  , Е z или Н r ,
, Е z или Н r ,  , Н z) есть краткая форма от величин Е i (r, φ, z) и Н i (r, φ, z),
, Н z) есть краткая форма от величин Е i (r, φ, z) и Н i (r, φ, z),
где i – координаты r, φ или z в цилиндрической системе координат.
Так как поперечные составляющие могут быть выражены через продольные, то решение скалярных уравнений для проекций 

является достаточным для определения всех составляющих векторов 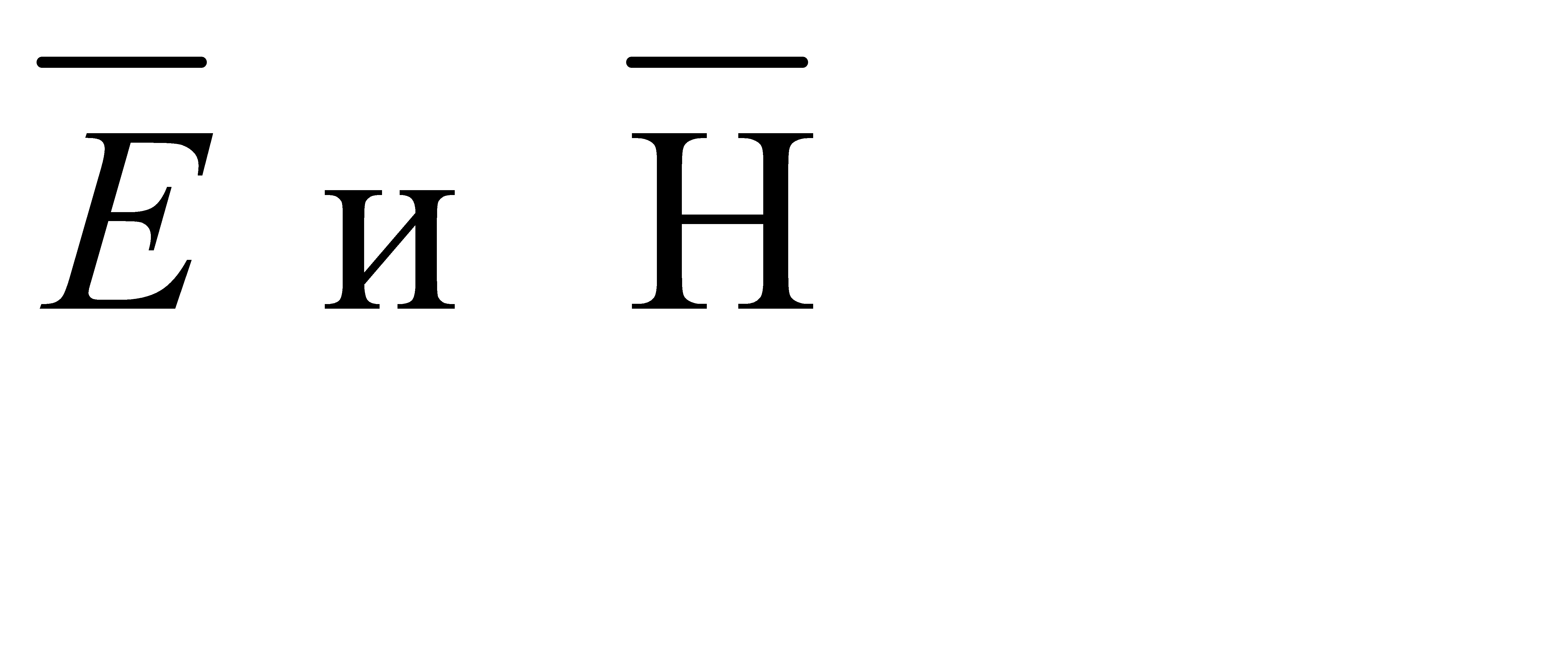 электромагнитного поля.
электромагнитного поля.
С учетом координатного выражения оператора Лапласа

из уравнений (16) и (17) получим дифференциальные уравнения второго порядка для продольных составляющих  в цилиндрической системе координат в виде:
в цилиндрической системе координат в виде:

В различных средах напряженность волн электромагнитного поля, бегущих в направлении оси Z, изменяется по экспоненциальному закону  , где А - любая составляющая векторов
, где А - любая составляющая векторов 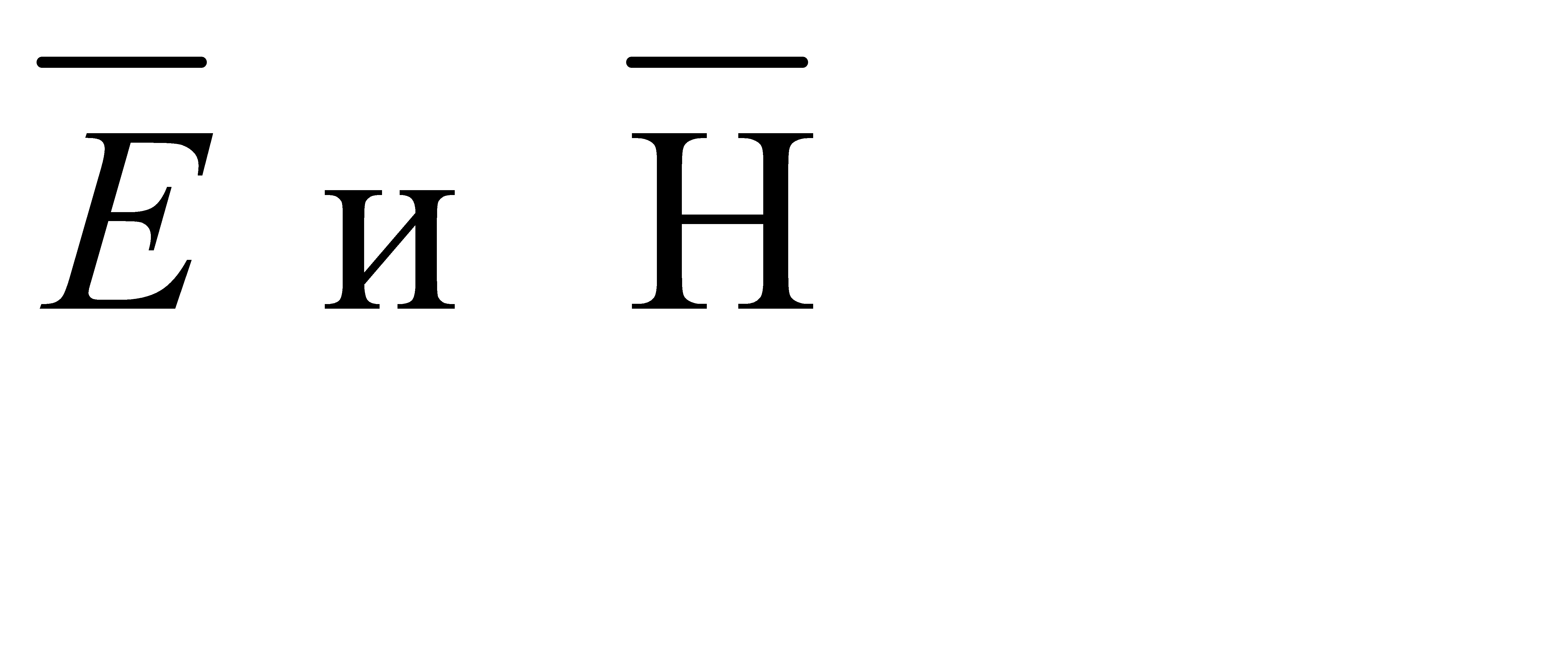 ;
;  – начальная составляющая векторов
– начальная составляющая векторов 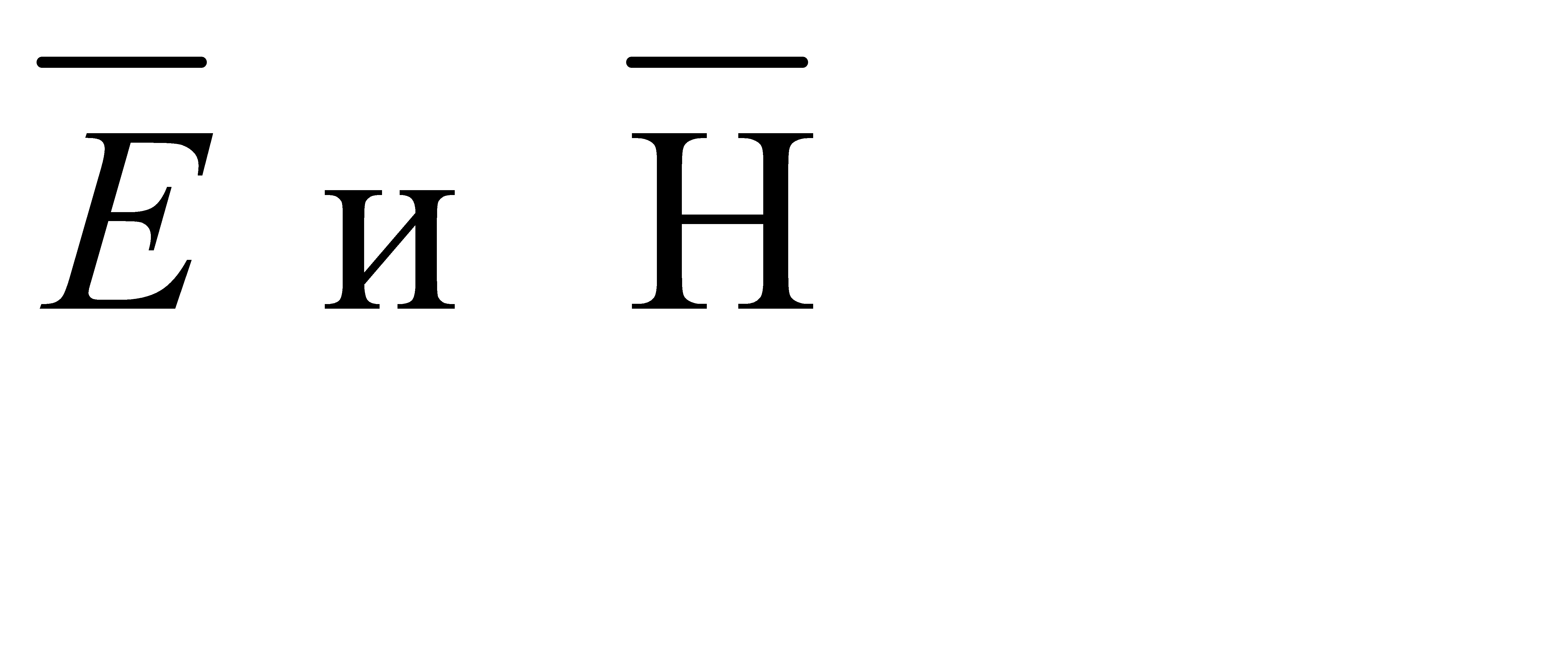 ; γ – коэффициент распространения волны вдоль направляющей системы (линии).
; γ – коэффициент распространения волны вдоль направляющей системы (линии).
Первая и вторая производные соответственно:
 .
.
Подставляя значение второй производной в выражения (18) и (19), получим:

где  . (22)
. (22)
Уравнения (20) и (21) характеризуют продольные составляющие полей при их распространении по цилиндрическим направляющим системам. Полученные уравнения справедливы в общем виде для продольных составляющих электрических, магнитных и смешанных волн. Поперечные составляющие полей можно определить через продольные составляющие, используя координатное разложение уравнений системы (2).



 , где
, где  .
. . (3)
. (3) , (4)
, (4) – оператор Лапласа и вводя обозначение
– оператор Лапласа и вводя обозначение . (5)
. (5) = 0, получим
= 0, получим (6)
(6) характеризует затухание комплексных амплитуд
характеризует затухание комплексных амплитуд  и поэтому называется коэффициентом затухания, а величина
и поэтому называется коэффициентом затухания, а величина  , характеризующая фазу (задержку во времени), носит название коэффициента фазы.
, характеризующая фазу (задержку во времени), носит название коэффициента фазы. (7)
(7) и называются волновыми уравнениями в векторной форме.
и называются волновыми уравнениями в векторной форме. , удовлетворяющий уравнению (7), можно найти
, удовлетворяющий уравнению (7), можно найти 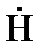 из второго уравнения системы (2) по формуле:
из второго уравнения системы (2) по формуле:
 не зависят от координат точек пространства. Примером однородной среды является диэлектрик. Волна называется плоской и однородной, если ее гармонические векторы зависят только от одной координаты, при этом в электромагнитном поле можно провести ряд параллельных плоскостей, перпендикулярных направлению распространения волны так, чтобы векторы напряженности
не зависят от координат точек пространства. Примером однородной среды является диэлектрик. Волна называется плоской и однородной, если ее гармонические векторы зависят только от одной координаты, при этом в электромагнитном поле можно провести ряд параллельных плоскостей, перпендикулярных направлению распространения волны так, чтобы векторы напряженности  в каждый момент времени лежали в этих плоскостях и сохраняли как свое значение, так и направление вдоль всей плоскости. Основным свойством плоской волны является взаимная перпендикулярность векторов
в каждый момент времени лежали в этих плоскостях и сохраняли как свое значение, так и направление вдоль всей плоскости. Основным свойством плоской волны является взаимная перпендикулярность векторов 
 , (8)
, (8) обозначена комплексная амплитуда
обозначена комплексная амплитуда  .
. уравнение (8) приобретает вид
уравнение (8) приобретает вид (9)
(9) (10)
(10) ), другую в обратном направлении – отраженная волна (
), другую в обратном направлении – отраженная волна ( ), что обусловлено выбором временного множителя в виде
), что обусловлено выбором временного множителя в виде  .
. и при
и при  - проводником. Некоторые среды (почва, вода) в диапазоне нижних частот обнаруживают проводниковые свойства, а выше – изолирующие.
- проводником. Некоторые среды (почва, вода) в диапазоне нижних частот обнаруживают проводниковые свойства, а выше – изолирующие. (11)
(11) , а коэффициент фазы
, а коэффициент фазы  .
. (12)
(12) , т.е. совпадает со скоростью света.
, т.е. совпадает со скоростью света. , поэтому в любой точке поля плоской волны в вакууме отношение напряженности электрического поля к напряженности магнитного поля постоянно и равно
, поэтому в любой точке поля плоской волны в вакууме отношение напряженности электрического поля к напряженности магнитного поля постоянно и равно  .
. .
.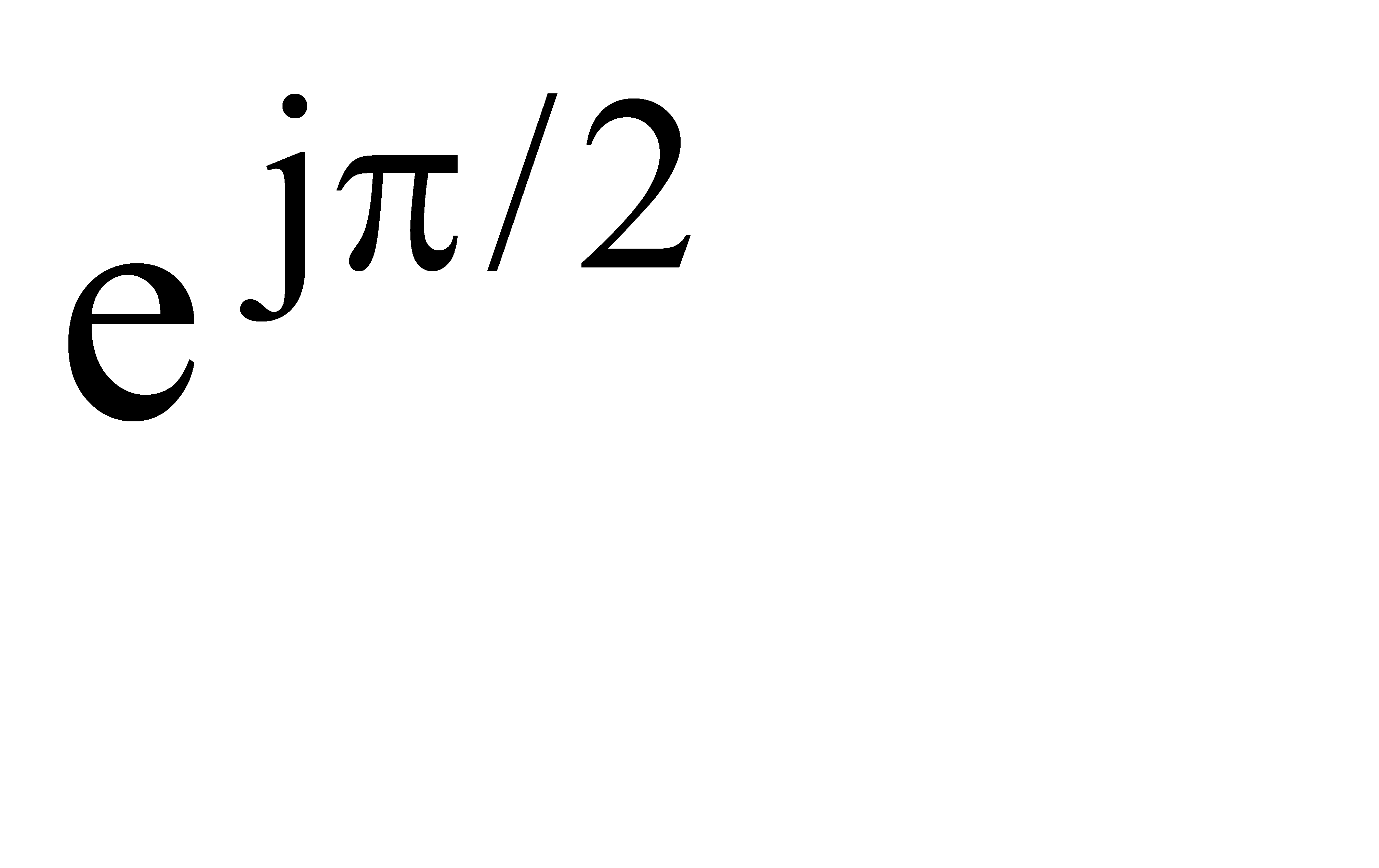 , получим что коэффициент затухания равен коэффициенту фазы
, получим что коэффициент затухания равен коэффициенту фазы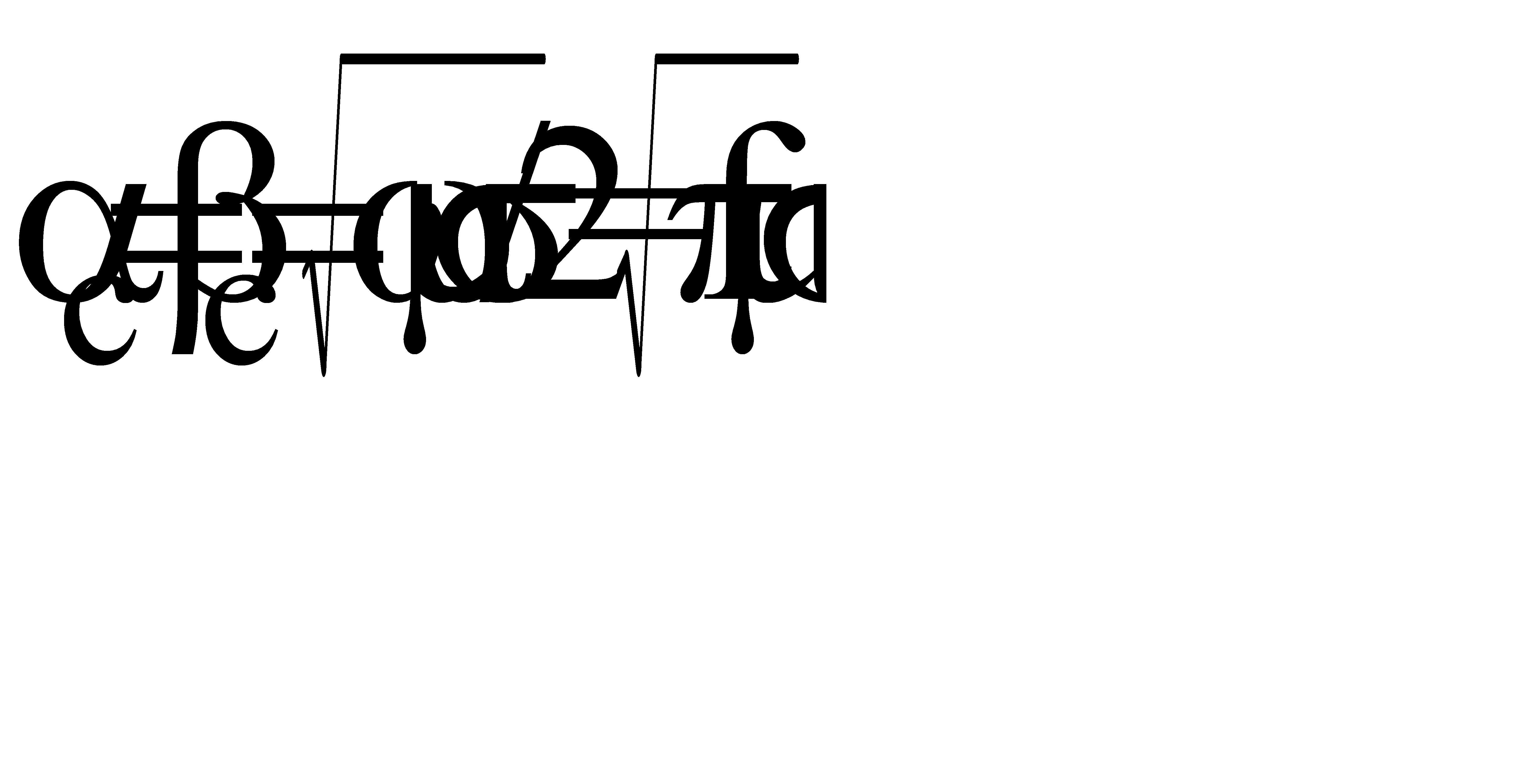 . (13)
. (13) . Если задаться уменьшением напряженности поля в е = 2,71 раза на глубине
. Если задаться уменьшением напряженности поля в е = 2,71 раза на глубине  от поверхности проводника, то эта глубина определится из условия
от поверхности проводника, то эта глубина определится из условия 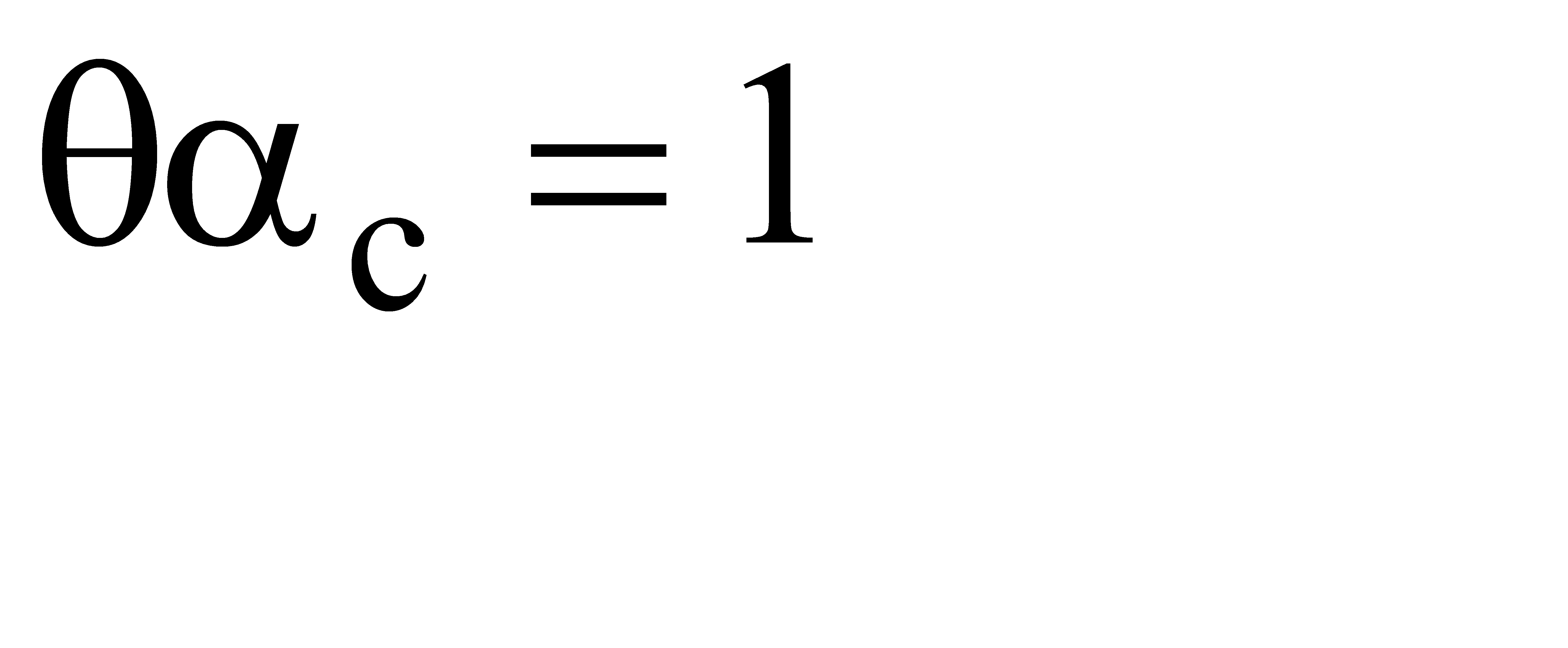 . Тогда
. Тогда  . Параметр
. Параметр  принято называть эквивалентной глубиной проникновения поля.
принято называть эквивалентной глубиной проникновения поля.

 ) и магнитного (
) и магнитного ( ) полей в данной точке пространства. Z
) полей в данной точке пространства. Z , (14)
, (14) , (15)
, (15)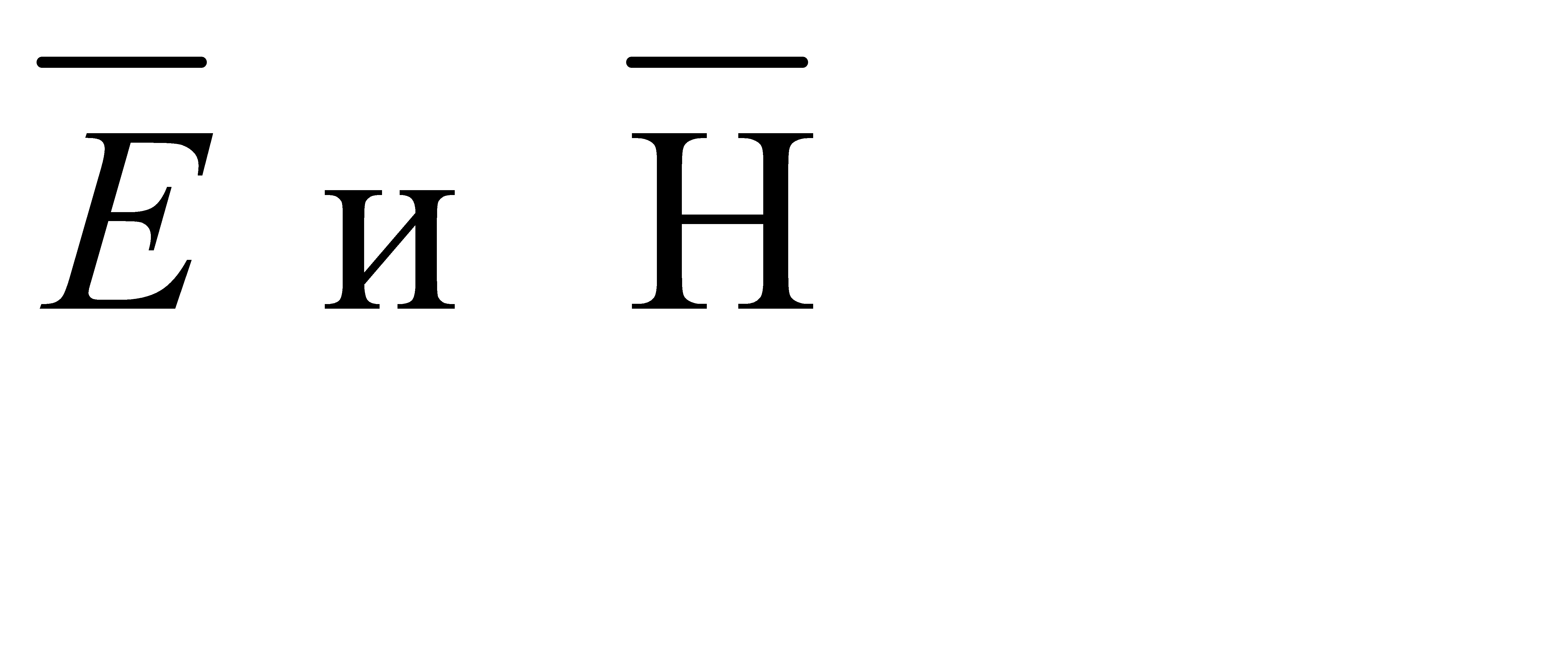 . Используемые в дальнейшем обозначения составляющих (Е r ,
. Используемые в дальнейшем обозначения составляющих (Е r ,  , Е z или Н r ,
, Е z или Н r ,  , Н z) есть краткая форма от величин Е i (r, φ, z) и Н i (r, φ, z),
, Н z) есть краткая форма от величин Е i (r, φ, z) и Н i (r, φ, z),


 в цилиндрической системе координат в виде:
в цилиндрической системе координат в виде:
 , где А - любая составляющая векторов
, где А - любая составляющая векторов  – начальная составляющая векторов
– начальная составляющая векторов  .
.
 . (22)
. (22)

